Micro-macro transitions in the atomic chain
Collaborator: W. Dreyer
(FG 7),
M.
Herrmann
(FG 7),
J.
Sprekels
(FG 1)
Cooperation with: A. Mielke (Universitšt Stuttgart)
Supported by: DFG: Priority Program ``Analysis, Modellbildung und
Simulation von Mehrskalenproblemen'' (Analysis, modelling and
simulation of multiscale problems)
Description:
During the period of this report, we have studied micro-macro transitions for
the (nonlinear) atomic chain in the context of modulation theory. We have
focused on the following problems.
- We apply the ideas of classic modulation theory to the nonlinear atomic chain.
- We study the thermodynamic properties of the resulting modulation
equations including an equation of state and a corresponding Gibbs equation.
- We consider special atomic interaction potentials and derive the
corresponding modulation equations.
In this project we closely collaborate with the group of A. Mielke, University
of Stuttgart.
The atomic chain consists of N identical particles, labeled by
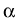 = 1..N, which are located at their positions
x
= 1..N, which are located at their positions
x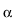 (t). The dynamics of
the chain is described by Newton's equation
(t). The dynamics of
the chain is described by Newton's equation
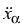 (t) = (t) = 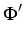 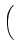 x x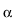 +1(t) - x +1(t) - x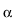 (t) (t) - - 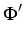 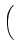 x x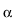 (t) - x (t) - x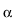 -1(t) -1(t)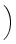 , ,
|
(1) |
where 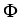 denotes a convex interaction potential. In order to pass to the
thermodynamic limit
N
denotes a convex interaction potential. In order to pass to the
thermodynamic limit
N 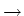
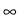 , we introduce a scaling
parameter
, we introduce a scaling
parameter
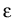 = 1/N and we define the macroscopic time
= 1/N and we define the macroscopic time
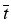 and particle index
and particle index
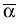 by
In contrast to the macroscopic variables, we interpret t and
by
In contrast to the macroscopic variables, we interpret t and 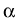 as the
microscopic time and particle index, respectively.
as the
microscopic time and particle index, respectively.
The general strategy of modulation theory is as follows:
- We identify a family of special solutions of (1), which are
parametrized by a finite number of parameters. In the case at hand, the
special solutions are traveling waves.
- We modulate the parameters on the macroscopic scale, so that there
result at least approximate solutions of (1). There exist
modulation restrictions in form of macroscopic PDEs.
A traveling wave for the atomic chain has parameters r, v, k,
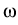 and can be written as
and can be written as
Here,
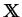
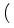
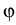
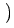 is the 1-periodic wave
profile, which describes the microscopic oscillations. Since the wave profile
depends on r, v, k, and
is the 1-periodic wave
profile, which describes the microscopic oscillations. Since the wave profile
depends on r, v, k, and 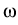 , we write
, we write
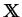 (r, v, k,
(r, v, k, 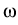 ;
; 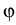 ).
).
A modulated traveling wave results, if we allow variations of the
traveling wave parameters on the macroscopic scale. More precisely, we set
x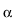 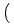 t t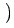 |
= |
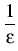 X( X(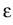 t, t, 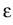 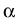 ) + ) + 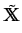 ( (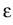 t, t, 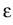 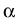 ; ; 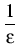 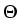 ( (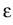 t, t, 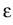 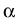 ;)), ;)), |
(4) |
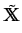 ( (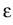 t, t, 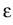 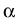 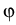 ) ) |
= |
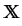 (r( (r(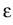 t, t, 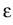 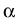 ), v( ), v(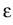 t, t, 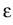 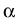 ), k( ), k(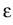 t, t, 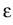 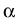 ), ), 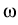 ( (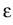 t, t, 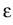 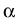 )), )), |
(5) |
where
v = 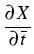 , r = , r = 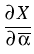 , ,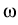 = = 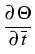 , andk = , andk = 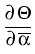 . .
|
(6) |
The modulation equations govern the macroscopic evolution of the fields r,
v, k, and 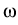 and ensure that the ansatz (4)
provides approximate solutions satisfying (1) up to order
and ensure that the ansatz (4)
provides approximate solutions satisfying (1) up to order
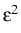
 . The modulation equations
read
There is an immediate physical interpretation of all quantities: r
- specific
length, v - mean velocity, p - pressure, k - wave number,
. The modulation equations
read
There is an immediate physical interpretation of all quantities: r
- specific
length, v - mean velocity, p - pressure, k - wave number,
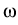 -
frequency, S - specific entropy density, g - entropy flux. Consequently, the
four equations in (7) are the macroscopic conservation
laws for mass, momentum, wave number, and entropy. The system is closed by
means of a Gibbs equation
-
frequency, S - specific entropy density, g - entropy flux. Consequently, the
four equations in (7) are the macroscopic conservation
laws for mass, momentum, wave number, and entropy. The system is closed by
means of a Gibbs equation
dE = v dv + 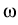 dS - p dr - g dk. dS - p dr - g dk.
|
(8) |
Here, E abbreviates the specific total energy, which is given by an equation
of state
E = E(r, v, k, 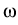 ). Unfortunately, the equation of
state is given only implicitly, and thus a complete understanding of the
modulation equations needs more insight into the structure of traveling
waves. However, there exist some special atomic interaction potentials
). Unfortunately, the equation of
state is given only implicitly, and thus a complete understanding of the
modulation equations needs more insight into the structure of traveling
waves. However, there exist some special atomic interaction potentials 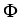 ,
for which the equation of state can be calculated explicitly:
,
for which the equation of state can be calculated explicitly:
- the harmonic potential;
- the case of hard sphere collisions;
- a model of elastic collision that combines the cases 1 and
2;
- the limit of small amplitudes.
References:
- W. DREYER, M. KUNIK,
Cold, thermal and oscillator closure of the atomic chain,
J. Phys. A, Math. Gen., 33 (2000), pp. 2097-2129.
- W. DREYER, M. HERRMANN, A. MIELKE,
Micro-macro transition for the atomic chain
via Whitham's modulation equation,
Preprint no. 119 of DFG Priority Program ``Analysis, modelling and
simulation of multiscale problems'',
Universität Stuttgart, 2004, submitted.
- A.-M. FILIP, S. VENAKIDES,
Existence and modulation of traveling waves in particle chains,
Commun. Pure Appl. Math., 51 (1998), pp. 693-736.
- G.B. WHITHAM,
Linear and Nonlinear Waves, vol. 1237 of
Pure And Applied Mathematics,
Wiley Interscience, New York, 1974.
LaTeX typesetting by I. Bremer
2004-08-13
![]() = 1..N, which are located at their positions
x
= 1..N, which are located at their positions
x![]() (t). The dynamics of
the chain is described by Newton's equation
(t). The dynamics of
the chain is described by Newton's equation
![]() and can be written as
and can be written as