[Next]:  Low temperature phases in models with  
 [Up]:  Project descriptions  
 [Previous]:  Project descriptions  
 [Contents]   [Index] 

Stochastic dynamics

Collaborator: A. Bovier , B. Gentz

Cooperation with: G. Ben Arous (Courant Institute, New York, USA), N. Berglund (Centre de Physique Théorique, Marseille, and Université de Toulon, France), M. Eckhoff (University of Zürich, Switzerland), V. Gayrard (Centre de Physique Théorique, Marseille, France, and Ecole Polytechnique Fédérale, Lausanne, Switzerland), M. Klein (Universität Potsdam)

Description:

The central issue that is addressed in this project is how to adequately describe a complex system whose dynamics is specified on a microscopic scale on spatially coarsened macro- or mesoscopic scales in terms of an effective dynamics on different time scales inherent to the system. The emphasis here is to be put on the fact that these effective dynamics must depend, in general, on the time scale considered. For example, while even in microscopically stochastic systems one expects generally deterministic limit dynamics for the spatially coarsened system on short time scales (homogenization), on much longer time scales stochastic effects may again become relevant and may even appear in deterministic systems as a residual effect of the integrated short-wavelength degrees of freedom.

One of the central concepts in this context is that of metastability. It applies to situations where the state space of a system can be decomposed into several (``quasi-invariant'') subsets in which the process remains for a very long time before transiting from one such set into another. Over the last years, we have developed a novel approach to the analysis of both probabilistic (distribution of transition times) and spectral (eigenvalues and eigenfunctions of the generator) quantities and their relations. This approach allows in particular to obtain rigorous results that have a far greater precision than the standard exponential estimates obtained in the Wentzell-Freidlin theory. In the past year, the results for discrete Markov chains obtained in [5] have been extended to diffusion processes in the continuum [6], [7]. The processes we consider have generators of the form

\begin{displaymath} l_\varepsilon=-\varepsilon\Delta+\nabla F\cdot\nabla\end{displaymath}

where F is a real valued, smooth function on a regular subset of $\IR^d$. Here $\varepsilon\gt$ is a small parameter. In this setting metastable behavior arises when F has several local minima. In this setting, we are able to again relate in a precise way metastable mean exit times to the small eigenvalues of the Markov generator. These eigenvalues are in turn related to the eigenvalues of a classical capacity matrix, associated to a capacitor made of small balls centered around the local minima of F. Using variational inequalities, it turns out that the relevant capacities can be computed in this case precisely up to multiplicative errors tending to one as $\varepsilon\downarrow 0$, under some non-degeneracy conditions on the function F. This allowed to give the first rigorous proof of some classical formulas attributed to Eyring [8] and Kramers [10]. A by-product of our proofs provides also very sharp estimates on the eigenfunctions corresponding to the exponentially small eigenvalues that allow to identify the ``valley-structure'' of the function F from the analysis of these eigenfunctions. We expect these results to be useful in the numerical domain decomposition methods initiated in [9].

On a second line, we continued our study of the combined effect of a slowly changing parameter and noise on dynamical systems. As already reported last year, we developed a new approach to one-dimensional systems with a slowly time-dependent parameter, [1], [2], [3]. This year, we successfully extended the method to multi-dimensional systems where the parameter itself may evolve according to a stochastic differential equation. This leads to a general class of fully coupled stochastic slow-fast systems

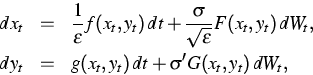
\begin{eqnarray*} dx_t & = & \frac{1}{\varepsilon} f(x_t,y_t)\,dt + \frac{\sigma... ...)\,dW_t, \ dy_t & = & g(x_t,y_t)\,dt + \sigma' G(x_t,y_t)\,dW_t,\end{eqnarray*}

where the fast variables xt, the slow variables yt, and the Brownian motion (Wt)t can be multi-dimensional. Such singularly perturbed stochastic differential equations are widely used in the sciences to model systems evolving on two well-separated time scales. Examples include systems containing heavy and light particles, predator-prey systems, and climate models like the Atlantic thermohaline circulation.

Under suitable assumptions on the associated deterministic system, we proved concentration results for the sample paths of the fast variables of the stochastic system. For small but finite values of the parameters $\varepsilon, \sigma, \sigma'$, the sample paths remain concentrated in a neighborhood of a so-called slow manifold at least up to a time of order one. Depending on the dynamics of the slow variables, such a result can hold considerably longer, up to exponentially long times, for instance when the slow variables of the deterministic system track an asymptotically stable periodic orbit. This allows to control the fluctuations of the fast variables due to noise and to study the (lower-dimensional) reduced dynamics on the slow manifold instead of the full system. In the important case when the slow manifold contains bifurcation points, we obtain similar concentration properties for the fast variables corresponding to non-bifurcating modes and conditions under which the system can be approximated by a lower-dimensional one, in which the fast variables contain only bifurcating modes [4].

References:

  1. N. BERGLUND, B. GENTZ, Pathwise description of dynamic pitchfork bifurcations with additive noise, Probab. Theory Related Fields, 122 (2002), pp. 341-388.
  2. \dito , A sample-paths approach to noise-induced synchronization: Stochastic resonance in a double-well potential, Ann. Appl. Probab., 12 (2002), pp. 1419-1470.
  3. \dito , The effect of additive noise on dynamical hysteresis, Nonlinearity, 15 (2002), pp. 605-632.
  4. \dito , Geometric singular perturbation theory for stochastic differential equations, WIAS Preprint no. 735, 2002, to appear in: J. Differential Equations.
  5. A. BOVIER, M. ECKHOFF, V. GAYRARD, M. KLEIN, Metastability and low-lying spectra in reversible Markov chains, Comm. Math. Phys., 228 (2002), pp. 219-255.
  6. \dito , Metastability in reversible diffusion processes I. Sharp asymptotics for capacities and exit times, WIAS Preprint no. 767, 2002, submitted.
  7. \dito , Metastability in reversible diffusion processes II. Precise asymptotics for small eigenvalues, WIAS Preprint no. 768, 2002, submitted.
  8. H. EYRING, The activated complex in chemical reactions, J. Chem. Phys., 3 (1935), pp. 107-115.
  9. W. HUISINGA, S. MEYN, CH. SCHÜTTE, Phase transitions and metastability for Markovian and molecular systems, Preprint, Freie Universität Berlin, 2002.
  10. H.A. KRAMERS, Brownian motion in a field of force and the diffusion model of chemical reactions, Physica, 7 (1940), pp. 284-304.


 [Next]:  Low temperature phases in models with  
 [Up]:  Project descriptions  
 [Previous]:  Project descriptions  
 [Contents]   [Index] 

LaTeX typesetting by I. Bremer
5/16/2003