Numerical simulation and optimization of SiC

[Next]:

Multiscale modeling of thermoelastic bodies

[Up]:

Project descriptions

[Previous]:

Optoelectronical sensors

[Contents]

[Index]

Numerical simulation and optimization of SiC single crystal growth by sublimation from the gas phase

Collaborator: O. Klein (FG 1), P. Philip (FG 1), J. Sprekels (FG 1), K. Wilmanski (FG 7)

Cooperation with: K. Böttcher, D. Schulz, D. Siche (Institut für Kristallzüchtung, Berlin)

Supported by: BMBF: ``Numerische Simulation und Optimierung der Züchtung von SiC-Einkristallen durch Sublimation aus der Gasphase'' (Numerical simulation and optimization of SiC single crystal growth by sublimation from the gas phase)

Description:

Owing to numerous technical applications in electronic and optoelectronic devices, such as lasers, semiconductors, and sensors, the industrial demand for high-quality SiC bulk single crystals remains large. It is still a challenging problem to grow sufficiently large SiC crystals with a low defect rate. Sublimation growth of SiC bulk single crystals via physical vapor transport (PVT), also known as the modified Lely method, has been one of the most successful and most widely used growth techniques of recent years.

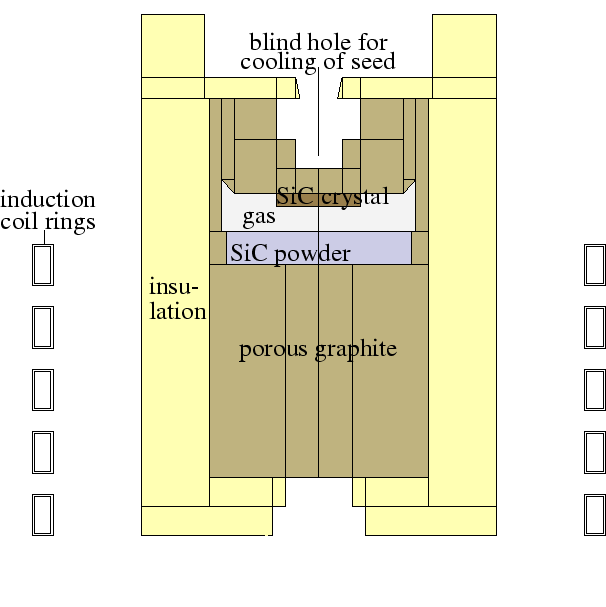
During PVT a graphite crucible (see Fig. 1) is placed in a low-pressure inert gas atmosphere consisting of argon. The crucible is then intensely heated, e.g., by induction heating , to temperatures of some 3000 K. Inside the crucible, polycrystalline SiC source powder is evaporated, resulting in a gas mixture consisting of argon and molecules made up of silicon and carbon, Si, $\text{Si}_2\text{C}$ , and $\text{SiC}_2$ being the predominant species. The SiC single crystal grows on an SiC single crystalline seed that is kept at a temperature below that of the SiC source. There is also a variant of PVT where tantalum is used as crucible material instead of graphite.

**Fig. 1:** Setup of growth apparatus according to [1]
$%% \ProjektEPSbildNocap {0.7\textwidth}{fb01_8_02_philip_setup.eps}$

Since reactor temperatures up to 3000 K make direct observations of the processes inside the growth chamber highly impractical, it is of paramount importance to have reliable theoretical models that allow the use of numerical simulation to improve the understanding of the growth procedure and to predict favorable growth conditions. Control parameters with respect to an optimization of the crystal growth are the design of the apparatus, the position of the induction coil, the heating power, and the inert gas pressure.

The physical and mathematical modeling of the growth process leads to a highly nonlinear system of coupled partial differential equations. In addition to the kinetics of a rare gas mixture at high temperatures, one has to consider heat transport by conduction and radiation, reactive matter transport through porous and granular media, and different kinds of chemical reactions and phase transitions. Moreover, several free boundaries occur in the model, e.g., due to the growing crystal and due to the evaporating source powder.

The model of the gas mixture is based on continuous mixture theory and results in balance equations for mass, momentum, and energy, including reaction-diffusion equations. The energy balance in the gas mixture is coupled to the different energy balance equations in the various solid components of the growth apparatus via suitable interface conditions ([2]).

Due to the high temperatures, it is essential to include heat transfer by radiation between surfaces of cavities in the growth apparatus. In our model we account for the radiative heat transfer using the net radiation model. The semi-transparency of the single crystal is included via the band approximation model ([3, 4]).

The heat sources caused by induction heating are computed via an axisymmetric complex-valued magnetic scalar potential that is determined as the solution of an elliptic PDE using the imposed voltage as input data. The scalar potential enables the resulting current density and thus the heat sources to be calculated. Within the research of 2001 we refined our induction heating model to ensure the correct computation of the voltage distributions to the coil rings during axisymmetric and sinusoidal modeling ([5]).

Building on previous work, within the research year 2001 the model was used to create the prototypical numerical simulation software WIAS-HiTNIHS. In its current version the software constitutes an effective tool to simulate the evolution of the temperature inside the growth apparatus including heat sources caused by induction heating, heat transport by diffusion, radiation, and constant convection in good agreement with physical experiments. It can thus be used to test and optimize geometrical setups with respect to favorable growth conditions. See [6] for an account of parameter studies varying heating voltage and coil positions.

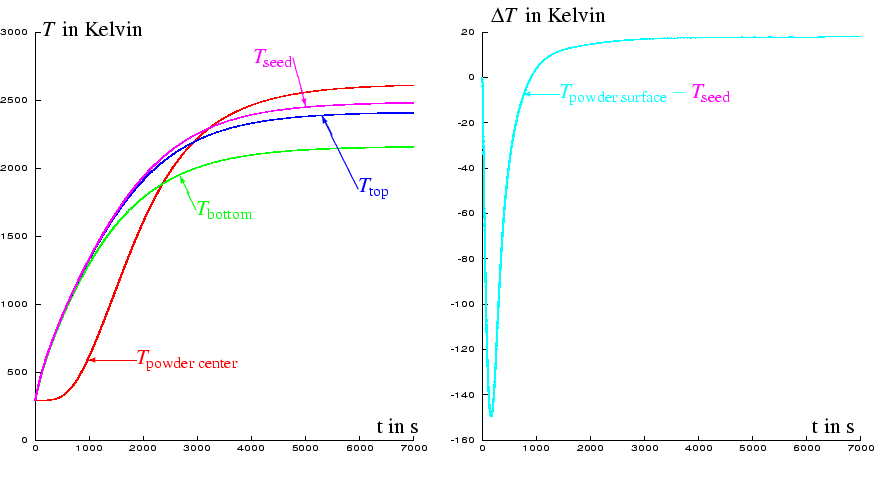
Figures 2 and 3 depict results of numerical simulations of the heating process for the configuration of Fig. 1.

On the left-hand side of Fig. 2 it can be seen that the evolution of the temperature in the center of the powder is quite different from $T_{\rm top}$ and $T_{\rm bottom}$ , i.e. from the temperatures that can be measured during the production process. The temperature $T_{\rm powder surface}$ is omitted in the left-hand figure, since in the depicted temperature scale it almost coincides with $T_{\rm seed}$ . The evolution of the difference between $T_{\rm powder surface}$ and $T_{\rm seed}$ is illustrated on the right-hand side of Fig. 2.

**Fig. 2:** Numerical results for the configuration of Fig. 1. Left-hand side: temperature evolution at the top and at the bottom ( $T_{\rm top}$ and $T_{\rm bottom}$ ), at the seed ( $T_{\rm seed}$ ), and in the center of the powder ( $T_{\rm powder center}$ ). Right-hand side: evolution of the temperature difference between powder surface and seed.
$%% \ProjektEPSbildNocap {1.0\textwidth}{fb01_8_02_philip_diagram.eps}$

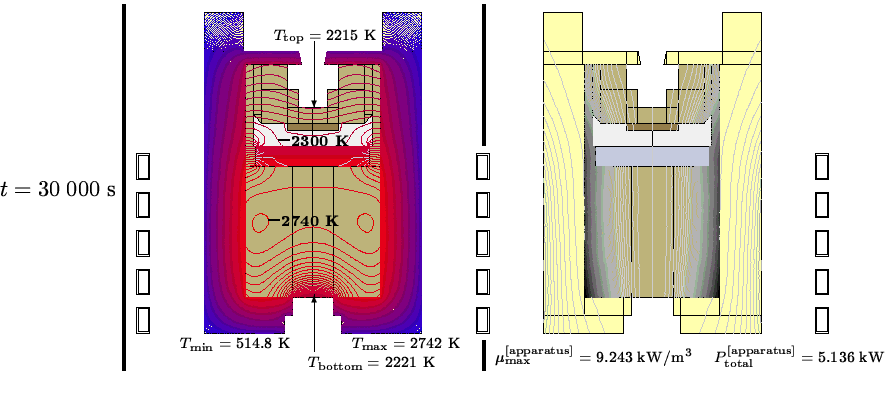
The computed temperature distribution and corresponding heat sources for the quasi-stationary state at the end of the heating process (t=30 000 s) are presented in Fig. 3. The temperature difference between neighboring isotherms in the left picture is 20 K. The minimal temperature $T_{\text{min}}$ occurs at the outside of the insulation, whereas the maximal temperature $T_{\text{max}}$ occurs inside the lower graphite body of the apparatus. In the right-hand picture the difference between isolevels is 0.1 kW/m $\mbox{}^3$ ,darker regions indicating larger heat sources. The depicted heat sources correspond to a total power $P_{\rm total}^{\rm [apparatus]}=5.136$ kW. The maximal power density $\mu_{\max}^{\rm [apparatus]}$ occurs in the lower outside corner of the graphite.

**Fig. 3:** Computed temperature distribution (left-hand side) and corresponding heat sources (right-hand side) at the end of the heating process for the configuration of Fig. 1
$%% \ProjektEPSbildNocap {1.0\textwidth}{fb01_8_02_philip_sim.eps.gz}$

References:

M. PONS, M. ANIKIN, K. CHOUROU, J.M. DEDULLE, R. MADAR, E. BLANQUET, A. PISCH, C. BERNARD, P. GROSSE, C. FAURE, G. BASSET, Y. GRANGE, State of the art in the modelling of SiC sublimation growth,
Materials Science and Engineering B, 61-62 (1999), pp. 18-28.
N. BUBNER, O. KLEIN, P. PHILIP, J. SPREKELS, K. WILMANSKI, A transient model for the sublimation growth of silicon carbide single crystals,
J. Crystal Growth, 205 (1999), pp. 294-304.
O. KLEIN, P. PHILIP, J. SPREKELS, K. WILMANSKI, Radiation- and convection-driven transient heat transfer during sublimation growth of silicon carbide single crystals,
J. Crystal Growth, 222 (2001), pp. 832-851.
O. KLEIN, P. PHILIP, Transient numerical simulation of sublimation growth of SiC single crystals,
in: Smart Materials, Proceedings of the 1st caesarium, Bonn, November 17-19, 1999, K.-H. Hoffmann, ed., Springer, Berlin, Heidelberg, 2001, pp. 127-136.
$\dito$ , Correct voltage distribution for axisymmetric sinusoidal modeling of induction heating with prescribed current, voltage, or power, WIAS Preprint no. 669, 2001, IEEE Trans. Magnetics, 38 (2002), pp. 1519-1523.
$\dito$ , Transient numerical investigation of induction heating during sublimation growth of silicon carbide single crystals, WIAS Preprint no. 659, 2001, submitted.