Modeling and simulation of blue-emitting semiconductor

[Next]:

Optoelectronical sensors

[Up]:

Project descriptions

[Previous]:

Envelope function approximation of electronic states

[Contents]

[Index]

Modeling and simulation of blue-emitting semiconductor nanostructures

Collaborator: U. Bandelow (FG 1), Th. Koprucki (FG 3)

Supported by: DFG: Priority Program ``Analysis, Modellierung und Simulation von Mehrskalenproblemen'' (Analysis, modeling and simulation of multiscale problems)

Description: Although diode lasers have existed for more than 25 years, blue-emitting diodes have only recently been realizable. This closed the ``gap'' between devices emitting in the visible spectral range and gives rise to many applications with a big market potential. Such applications include active laser tv, increasing storage capacities on DVDs and very high-quality laser printers.

The technological breakthrough to the blue laser diodes came with the successful epitaxy of GaN-based nanostructures. Typically, these materials grow in crystallographic wurtzite configurations and display a large energy band gap, as well as other unusual features.

We have simulated such nanostructures using the eight-band kp-model for wurtzite semiconductors in WIAS-QW. This model is a generalization of [1] including strain, spin-orbit interaction, and crystal-field splitting. A primary result of such kp-calculations is the subband structure (dependence of the energy on the in-plane wave vector $k_\Vert=(k_x,k_y)$ ), as depicted in Fig. 1.

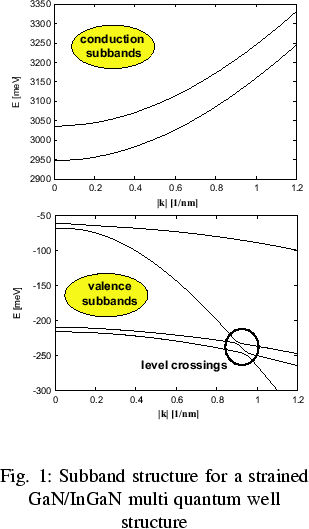$% latex2html id marker 29055 \minipage{0.45\textwidth}\begin{figure} %%\htmlima... ... for a strained GaN/InGaN multi quantum well structure} \end{figure}\endminipage$ As shown in Fig. 1, the subband structure exhibits some remarkable properties, which partially differ from those known from other laser materials:

No warping (no angular dependence of the energy) is observed.
The conduction subbands are nearly parabolic. This means low band mixing between conduction and valence bands, mainly due to the large band gap (see y-axes in Fig.1).
The valence subbands show a small curvature, indicating much higher hole masses than for other semiconductor laser materials. Also the in-plane heavy hole mass is high (1.96m₀ for GaN).
The valence subbands are nonparabolic, indicating the valence band mixing effects. Moreover, level crossings can be observed, see lower figure in Fig.1.

Furthermore, eight-band kp-calculations allow for a realistic prediction of the matrix elements for the optical interband transitions ([3]), which are a prerequisite for the calculation of the optical response function for such nanostructures.

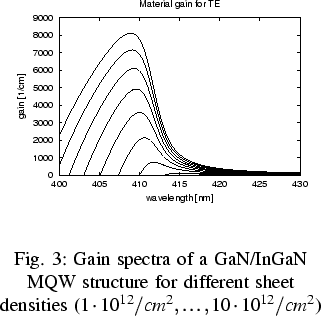$% latex2html id marker 29057 \minipage{0.48\textwidth}\begin{figure} %%\htmlima... ...s ($1\cdot 10^{12}/cm^2, \ldots, 10\cdot10^{12}/cm^2$)} \end{figure}\endminipage$ As a representation for the imaginary part of the optical response function, we have calculated the spectra of the optical material gain (TE-polarization has been assumed) for different sheet densities, as illustrated in Fig.2. The gain increases monotonically with the carrier density, but much higher densities are required for the laser threshold, compared to other semiconductor materials. This is mainly due to the much higher effective masses in GaN-based materials, as discussed above, but in some part also due to the reduced interband mixing.

Pure kp-calculations correspond to the exclusion of any Coulomb interaction between the carriers. Being charged fermions, their behavior can be drastically modified by such Coulomb effects. In particular, such impacts have been studied for GaN/InGaN quantum wells ([2]).

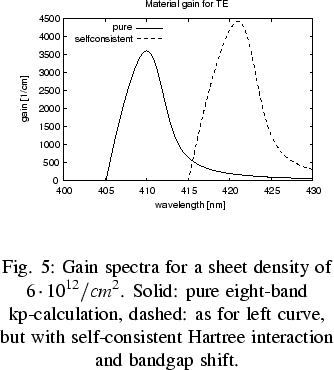
$% latex2html id marker 29058 \minipage{0.48\textwidth}\begin{figure} %%\htmlima... ...elf-consistent Hartree interaction and bandgap shift.} \end{figure}\endminipage$ For the calculation of some prominent Coulomb effects, we used a Kohn-Sham type model similar to [3], which has already been successfully applied to analyzing InP-based nanostructures. It includes the Hartree contribution via the Poisson equation and the bandgap shift via exchange-correlation potentials. As a result of such self-consistent calculations, the gain spectra experience a density-dependent red shift and a small enhancement, as observed by the difference between the curves in Fig.3. In addition, the electrons become more strongly confined, whereas the holes stay untouched in the self-consistent case. This is in contrast to the situation of InP-based nanostructures ([3]) and can be explained by the large heavy hole mass.

References:

S.L. CHUANG, C.S. CHANG $k\cdot p$ method for strained wurtzite semiconductors, Phys. Rev. B, 54 (1996), pp. 2491-2504.
H.-J. WÜNSCHE, F. HENNEBERGER, O. BRANDT, U. BANDELOW, H.-CHR. KAISER, Gain calculations for localized excitons and biexcitons: (In,Ga)N versus (Zn,Cd)Se quantum wells, 16th International Semiconductor Laser Conference (ISCL), Nara, Japan, 1998, Conference Digest, pp. 191-192.
U. BANDELOW, H.-CHR. KAISER, TH. KOPRUCKI, J. REHBERG, Modeling and simulation of strained quantum wells in semiconductor lasers, WIAS Preprint no. 582, 2000.