Numerical analysis of complex stochastic models

[Next]:

Research Group Continuum Mechanics

[Up]:

Project descriptions

[Previous]:

Applied mathematical finance

[Contents]

[Index]

Numerical analysis of complex stochastic models

Collaborator: P. Mathé , G.N. Milstein , K.K. Sabelfeld

Cooperation with: S. Orszag (Yale University, USA), T. Vesala (Helsinki University, Finland), P.K. Yeung (Georgian Institute of Technology, USA), O. Kurbanmuradov (Phys. Tech. Institute, Turkmenian Academy of Sciences, Ashkhabad), I.A. Shalimova (Institute of Computational Mathematics and Mathematical Geophysics, Russian Academy of Sciences, Novosibirsk), O. Smidts (Université Libre de Bruxelles, Belgium), G. Wei (Hong Kong Baptist University), M. Tretyakov (University of Wales, Swansea, UK)

Supported by: INTAS Project INTAS-99-1501, Nato Linkage Grant N 971664

Description:

Complex physical phenomena are conventionally governed by deterministic differential and integral equations, but the advanced measurements and modern technology require nowadays a development of stochastic research methods. The basis of these methods are stochastic models, so the main effort is often related to the creation of an adequate stochastic model which mimics, in a probabilistic sense, the desired physical phenomena. Next, these models should be efficiently modelled by computer. Mathematical analysis of the model and the implementation algorithm is an important part of research. A new type of stochastic model is developed for solving transport problems in saturated porous media which is the first stochastic Lagrangian model of Langevin type for porous media. We develop also stochastic algorithms for solving some examples of Cauchy and boundary value problems for nonlinear parabolic PDEs. The study is accomplished with an analysis of algorithms for high-dimensional integration.

1. Stochastic simulation models for transport in porous media (K.K. Sabelfeld).

It is well-known that stochastic models are well-developed for solving transport problems in turbulent flows like the transport in the atmospheric boundary layer (see, e.g., [24], [23]). This technique was extended to a wide class of flows, in particular, to rivers ([2]), to flows in porous media (see [4]). In the porous media transport, only one type of stochastic models was used, namely, the random displacement method (RDM) for hydrodynamic dispersion equations. It should be stressed that RDM can be applied only if the displacement covariance tensor is known (e.g., from measurements, or numerical simulation), and cannot be applied if the functionals of interest are evaluated at times comparable with the characteristic correlation scale of the flow. In contrast, the Lagrangian stochastic models based on the tracking particles in a random velocity field extracted from the numerical solution of the flow equation (for brevity, we will call this model DSM, the direct simulation method) are free of these limitations, but the computational resources required are vast. Therefore, we suggest to construct a Langevin-type stochastic model which is an approximation to DSM, and is written in the form of a stochastic differential equation for the position and velocity. It is worth to mention that the same scheme has been carried out in the atmospheric transport problem (see our recent work [8], [7], [26], [25] and [9]). The basis for the Langevin-type approach comes from the Kolmogorov similarity theory of fully developed turbulence ([22]) saying that the velocity structure tensor is a linear function in time which is universal in the inertial subrange. The linearity is the necessary condition to derive a Langevin-type equation to mimic the behavior of the real Lagrangian trajectories. Therefore, the crucial point is here to study if in the porous media , this kind of linear law can be observed. This problem is studied by the DSM. Detailed derivation of the Langevin-type model is given. Numerical simulations and comparisons with the random displacement model confirm that the new Lagrangian approach is highly efficient.

In many general flow conditions, the phenomenological Darcy law forms the basis of the theory of flow through porous media. It is a consequence of the linearity of the equations of slow viscous flow which are obtained from the Navier-Stokes equations by neglecting the inertial terms. For time-independent flow conditions and saturated porous media, it is written as

$\begin{displaymath} {\bf q}({\bf r}) = \theta({\bf r}) \, {\bf u}({\bf r}) = - K({\bf r}) \, {\bf \nabla} \phi({\bf r}),\end{displaymath}$

where ${\bf q}$ , $\theta$ , ${\bf u}$ , K, and $\phi$ are all macroscopic variables depending on space vector ${\bf r}$ , $\theta$ is the effective (or kinematic) porosity . This porosity takes into account the volumes of voids effectively concerned with ground-water flow (that is, for instance, without the dead-end pores and the adherence volume of the fluid to the grains). It is upper bounded by total porosity which is the volume occupied by the pores divided by the volume of the bulk medium, ${\bf q}$ is called Darcy's velocity and represents the ground-water flow rate, that is, the volume of water crossing a unit area of porous medium per unit time; ${\bf q}$ is a measurable quantity whereas ${\bf u}$ is the pore velocity, that is, the flow rate per unit area of fluid (which is equivalent to consider that only fluid is present). $\phi$ is the hydraulic potential (or pressure head). It is defined by $\phi = p/\rho g + z$ where p is the fluid pressure, $\rho$ the volumetric mass of the fluid, g the gravitational constant, and z the height. In $\phi$ , the kinematic term is always neglected due to small ground-water velocities in common applications. Finally, K, the proportionality coefficient between Darcy's velocity and the gradient of the hydraulic potential, is called hydraulic conductivity . This parameter (and also permeability) is recognized as a key parameter for ground-water flow. Several experimental techniques (of which mainly: pumping tests, sedimentary analysis, but also seismic, geoelectrical or tracer methods) are used to intensively measure this parameter in the laboratory or in the field scale. These measurements have put in evidence the (highly) heterogeneous behavior of K in space and have suggested the use of stochastic models.

In the stochastic models, the hydrogeological parameters (like K and $\theta$ ) are represented by Random Space Functions (RSF). A RSF h is regarded as a random variable with an infinite number of components. Thus, with the random function $h({\bf r})$ depending on the spatial coordinate ${\bf r}$ , h_i is defined as the value of h at a point r = r_i and the joint probability distribution function (Pdf) $F(h_1,h_2, \ldots,h_N)$ ,with $N \rightarrow \infty$ , contains the probability information about h. We can also regard $h({\bf r})$ as an ordinary function of the space coordinates in each realization and the ensemble underlying F, the Pdf, is that of the values of h at the set of points ${\bf r}_i$ ( $i=1,2, \ldots,N$ ).

Law ([10]) was the first to apply RSF in porous media and to propose, on the basis of core analysis data from a carbonate oil field reservoir, a log-normal probability density function (Pdf) for K. Since this proposition, there is now a large body of direct evidence to support the statement that the Pdf for hydraulic conductivity is log-normal ([1]), ([4]). Hydraulic log-conductivity $Y = \ln \, K$ is therefore commonly used and assumed to be distributed according to a Gaussian distribution $N(m_Y,\sigma_Y)$ , where m_Y = <Y>, and $\sigma_Y$ is the standard deviation.

Solving the Darcy equation with the random (log-normal) hydraulic conductivity, we have found the statistical characteristics required for the construction of the stochastic Lagrangian model in the form of a Langevin equation. The main difficulty was the unique derivation of this equation.

The results of the numerical simulation on the basis of the developed stochastic Lagrangian model are highly efficient, but what is especially important, is that the new model is free of many limiting assumptions used in the conventional models. In addition, the method calculates not only the mean concentration but also the flux of the concentrations.

2. A probabilistic approach to the solution of boundary value problems. Numerics for problems of stochastic dynamics (G.N. Milstein).

A probabilistic approach to constructing new numerical methods for solving Cauchy and boundary value problems for nonlinear parabolic PDEs is based on making use of the well-known probabilistic representations of solutions to linear PDEs and ideas of the weak sense numerical integration of SDEs. It takes into account a coefficients dependence on the space variables and a relationship between diffusion and advection in an intrinsic manner and allows to obtain a number of new effective numerical algorithms. The approach is applied to the numerical solution of the Dirichlet problem for nonlinear parabolic equations in [21].

In [15], some random walks for the general Dirichlet problem for linear elliptic and parabolic PDEs are proposed. They are based on the weak Euler approximation and on linear interpolation. Due to this, it is possible to suggest a number of efficient Monte Carlo algorithms.

Stochastic systems, phase flows of which have integral invariants, are considered in [16], [18], and [19]. In particular, the Hamiltonian systems perturbed by additive noise belong to systems with integral invariants. For such systems, numerical methods preserving a number of important features of the original phase flows are constructed. They demonstrate superiority in comparison with nonsymplectic methods in numerical experiments (see Fig. 1).

**Fig. 1:** A sample trajectory of a solution to an oscillator with noise obtained by the exact formulae (solid line), a symplectic method (points on the left figure), and the Euler method (points on the right figure). The symplectic and Euler methods are of the same order.
$\makeatletter \@ZweiProjektbilderNocap[h]{0.45\textwidth}{has1}{hae1} \makeatother$

Some theoretical and numerical investigations of stochastic systems connected with such phenomena as stochastic resonance and noise-induced unidirectional transport are reported in [20].

Stability properties of stochastic systems are studied in [5] and [17].

3. Monte Carlo and Quasi-Monte Carlo methods for integration (P. Mathé).

Many physically relevant quantities are means or require to compute certain means intermediately. Therefore, we investigate numerical methods for the efficient computation of integrals. Precisely, for a fixed probability $\pi$ on some space X, we aim at approximating $\int_{X}f(x)\; \pi(dx)$ by means of a sample mean of random variables arising from an ergodic Markov chain with transition kernel K, having $\pi$ as its invariant distribution. Thus, if $\nu$ is an initial distribution, then we use, for a given f on X, the sample mean

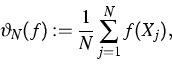
$\begin{displaymath} \vartheta_N(f):= \frac 1 N\sum_{j=1}^{N} f(X_{j}),\end{displaymath}$

where $X_{1},\dots,X_{N}$ are the consecutive steps of our Markov chain. Typically, the error is measured in mean square sense, i.e.

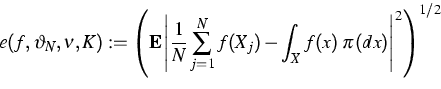
$\begin{displaymath} e(f,\vartheta_N,\nu,K):=\left(\mathbf E\left\vert \frac 1 N\... ...f(X_{j}) - \int_{X} f(x)\; \pi(dx) \right\vert^{2}\right)^{1/2}\end{displaymath}$

denotes the individual error of the sample mean at function f. Previous analysis, see [11], was restricted to uniformly ergodic Markov chains. It is, however, known that on general state space, most Markov chains will not be uniformly ergodic, see [6]. Therefore, as in [14], we extended our study to V-uniformly ergodic Markov chains. Another goal was to establish the interaction between ergodicity properties of the kernel K, respective classes F of functions to be integrated, and initial distributions $\nu$ .

Let $V\geq 1$ be a real valued function on X. By $L_\infty(V)$ we denote the Banach space of all functions f on X, for which $\Vert f \Vert _{V}:=\operatorname{ess-sup}\left\vert f(x)/V(x) \right\vert<\infty$ . The Harris-Markov chain K is called V-uniformly ergodic, if, for the transition operator $\operatorname{P}$ , we have

$\begin{displaymath} \Vert \operatorname{P}^n -\operatorname{E}\colon L_\infty(V)\to L_\infty(V) \Vert _{} \to 0.\end{displaymath}$

We established a series of consequences of this definition, using tools from interpolation theory. The intrinsic rôle of the weight function V became transparent.

Convergence results for the sample mean towards the integral are presented in terms of the following (quadratic) functional

$\begin{displaymath} \Phi(f):= \langle \pi,[(\operatorname{I}- \operatorname{P})^... ...atorname{E})f ][(\operatorname{I}- \operatorname{E})f] \rangle.\end{displaymath}$

A typical result can be stated as follows. For all initial distributions $\nu$ with $\int V(x)\;\nu(dx)<\infty$ and bounded sets F in the weighted Hilbert space L₂(V) we have

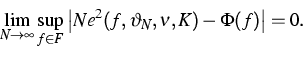
$\begin{displaymath} \lim_{N\to\infty}\sup_{f\in F}\left\vert Ne^{2}(f,\vartheta_{N},\nu,K) - \Phi(f) \right\vert=0. \end{displaymath}$

The convergence results are then extended to classes of functions which are no longer square integrable.

A further aspect was the study of QMC methods for functions over unbounded domains, in particular integrals ${\rm Int}_{\rho}(f):= \int f(\mathbf x)\rho(\mathbf x)\;d\mathbf x$ over $\IR^d$ with probability weight function $\rho$ . These can be evaluated with the aid of QMC algorithms using a proper decomposition of the domain $\IR^d$ and arrangement of the low discrepancy points over a series of hierarchical hypercubes. Precisely, we proposed

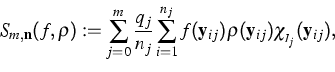
$\begin{displaymath} S_{m,\mathbf n}(f,\rho):=\sum_{j=0}^m \frac{q_j}{n_j}\sum_{i... ...hbf y_{ij})\rho(\mathbf y_{ij})\chi_{_{I_j}}(\mathbf y_{ij}), \end{displaymath}$

where m+1 is any number of cubes and $\mathbf n:=(n_0,\dots,n_m)$ , where each n_j is the number of points used within cube $Q_j,\ j=0,\dots,m$ , and the $\chi_{_{I_j}}$ are the indicator functions of $I_j:=Q_{j+1}\setminus Q_j$ . Furthermore,

$\begin{eqnarray*} q_j & = & \mbox{ Volume} (Q_j) = 2^{(j+1)d},\ \mathbf y_{ij}... ...}: 1\leq i\leq n_j}\right\} \subset [0,1]^d,\;\; 0\leq j \leq m.\end{eqnarray*}$

The total amount of function evaluations is $N=\sum_{j=0}^m n_j$ . The P_j s are some low-discrepancy point sets, consisting of n_j points, respectively.

By arranging the number of hypercubes as well as the number of low-discrepancy points properly, the proposed method can be seen to be optimal for power/exponential decaying weights. This was joint work with G. Wei, Hong Kong Baptist University, see [13]. Emphasis was on results which allow application to mathematical finance. Therefore we could assume smooth weights, but less smoothness for the integrands, in order to cover the evaluation of financial products.

References:

G. DAGAN, Flow and Transport in Porous Formations, Springer, New York, 1989.
C. ENGELHARD, O. KURBANMURADOV, K. SABELFELD, A. SUKHODOLOV. Numerical study of the statistical characteristics of the mixing processes in rivers, WIAS Preprint no. 705, 2001.
R.A. FREEZE, A stochastic-conceptual analysis of one-dimensional groundwater flow in nonuniform homogeneous media, Water Resources Research, 11 (1975), pp. 725-741.
L.W. GELHAR, Stochastic Subsurface Hydrology, Prentice Hall, New Jersey, 1993.
P. IMKELLER, G.N. MILSTEIN, The moment Lyapunov exponent for conservative systems with small periodic and random perturbations, WIAS Preprint no. 647, 2001.
S.F. JARNER, E. HANSEN, Geometric ergodicity of Metropolis algorithms, Stochastic Process. Appl., 85 (2000), pp. 341-361.
A. KOLODKO, K. SABELFELD, Stochastic Lagrangian model for spatially inhomogeneous Smoluchowski equation governing coagulating and diffusing particles, WIAS Preprint no. 689, 2001, to appear in: Math. Comput. Simulation.
O. KURBANMURADOV, Y. RANNIK, K. SABELFELD, T. VESALA, Estimation of mean concentration and fluxes by Lagrangian stochastic models, Math. Comput. Simulation, 54 (2001), pp 459-476.
O. KURBANMURADOV, S.A. ORSZAG, K. SABELFELD, P.K. YEUNG, Analysis of relative dispersion of two particles by Lagrangian stochastic models and DNS methods, Monte Carlo Methods and Applications, 7 (2001), pp. 245-264.
J. LAW, A statistical approach to the interstitial heterogeneity of sand reservoirs, Trans. AIME, 155 (1944), pp. 202-222.
P. MATHÉ, Numerical integration using Markov chains, Monte Carlo Meth. Appl., 5 (1999), pp. 325-343.
$\dito$ , Numerical integration using V-uniformly ergodic Markov chains, manuscript, 2001.
P. MATHÉ, G. WEI, Quasi-Monte Carlo integration over $\IR^d$ , manuscript, 2001.
S.P. MEYN, R.L. TWEEDIE, Markov Chains and Stochastic Stability, Springer, London, 1993.
G.N. MILSTEIN, The simplest random walk for the general Dirichlet problem, in: Stochastic Numerics Conference, February 19-21, Zürich, 2001, pp. 73-81.
$\dito$ , Symplectic integration of Hamiltonian systems with noise, Workshop on Computational Stochastic Differential Equations, March 26-30, 2001, University of Warwick, Coventry, UK.
$\dito$ , The asymptotic behavior of semi-invariants for linear stochastic systems, WIAS Preprint no. 675, 2001.
G.N. MILSTEIN, YU.M. REPIN, M.V. TRETYAKOV, Symplectic methods for Hamiltonian systems with additive noise, WIAS Preprint no. 640, 2001.
$\dito$ , Mean-square symplectic methods for Hamiltonian systems with multiplicative noise, WIAS Preprint no. 670, 2001.
G.N. MILSTEIN, M.V. TRETYAKOV, Noise-induced unidirectional transport, Stoch. Dyn., 1 (2001), pp. 361-375.
$\dito$ , Numerical solution of the Dirichlet problem for nonlinear parabolic equations by a probabilistic approach, IMA J. Numer. Anal., 21 (2001), pp. 887-917.
A.S. MONIN, A.M. YAGLOM, Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 1 and 2, The M.I.T. Press, 1981.
H. RODEAN, Stochastic Lagrangian Models of Turbulent Diffusion, Meteorological Monographs, 26, American Meteorological Society, Boston, 1996.
K. SABELFELD, Monte Carlo Methods in Boundary Value Problems, Springer, New York [and others], 1991.
K. SABELFELD, I. SHALIMOVA. Forward and backward stochastic Lagrangian models for turbulent transport and the well-mixed condition, Monte Carlo Methods and Applications, 7 (2001), pp. 369-382.
$\dito$ ,Random Walk on Spheres methods and iterative solutions of elasticity problems, WIAS Preprint no. 704, 2001.