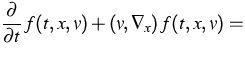Efficient control of stochastic particle methods

[Next]:

Research Group Stochastic Algorithms and Nonparametric

[Up]:

Project descriptions

[Previous]:

Stochastic particle systems as numerical tools

[Contents]

[Index]

Efficient control of stochastic particle methods for rarefied gas flows

Collaborator: W. Wagner , A. Eibeck , I. Matheis

Cooperation with: K. Aoki (Kyoto University, Japan), S. Ermakov (St. Petersburg University, Russia), A. Garcia (San Jose State University, USA), C. Lécot (Université de Savoie, Chambéry, France), S. Rjasanow (Universität des Saarlandes, Saarbrücken), S. Ukai (Yokohama National University, Japan)

Supported by: DFG: ``Effektive Steuerung von stochastischen Partikelverfahren für Strömungen in verdünnten Gasen'' (Effective control of stochastic particle methods for rarefied gas flow)

Description: Rarefied gas flows play an important role in applications like aerospace design (space shuttle reentry), vacuum engineering (material processing, pumps), or, more recently, nanotechnology. Mathematically, such flows are described (in the simplest case of a monatomic gas) by the Boltzmann equation

$\displaystyle{ \frac{\partial}{\partial t}\, f(t,x,v) + ( v,\nabla_x) \,f(t,x,v) = }$			(1)
		$\displaystyle\int_{{\mathbb R}^3}dw \int_{S^2} de \,B(v,w,e) \, \Big[f(t,x,v^)\,f(t,x,w^)-f(t,x,v)\,f(t,x,w)\Big]\,,$

where

$\begin{displaymath} v^*=v+e\,( e,w-v)\,, \quad w^*=w+e\,( e,v-w)\,.\end{displaymath}$

(2)

The solution f(t,x,v) represents the relative amount of gas molecules with velocity v at position x and time $t\,.$ The quadratic nonlinearity in (1) corresponds to the pairwise interaction between gas particles, which consists in the change of velocities of two particles according to (2). Here S² denotes the unit sphere in the Euclidean space ${\mathbb R}^3\,,$ and B is called the collision kernel, containing information about the assumed microscopic interaction potential.

Due to the high dimensionality of the problem (f is a function of 7 independent variables), stochastic algorithms are a commonly used tool for the numerical treatment of equation (1). Stochastic particle methods, like the standard DSMC (direct simulation Monte Carlo) technique, are based on the simulation of an appropriate large $(n\sim 10^6-10^7)$ system of particles

$\begin{displaymath} \Big(x_i(t),v_i(t)\Big)\,, \quad i=1,\ldots,n\,,\quad t\ge 0\,, \end{displaymath}$

approximating the behavior of the real gas. Here $x_i(t)\!\in\! D\!\subset\!{\mathbb R}^3$ and $v_i(t)\!\in\!{\mathbb R}^3$ denote the position and the velocity of the i-th particle at time $t\,.$

Stochastic particle methods for kinetic equations like (1) provide results which are subject to random fluctuations. Thus, the construction of algorithms with reduced fluctuations is an important problem (variance reduction problem). The main purpose of the project is to contribute to this field of research.

In recent years a new approach to the variance reduction problem has been developed, which is based on an alternative interaction mechanism. In [3] an extension of this so-called stochastic weighted particle method for the numerical treatment of the Boltzmann equation is presented. A new procedure for modeling the inflow boundary condition is introduced, which contains an appropriate control mechanism for the particle flow. Its performance is tested in a two-dimensional example with strong density gradients. A gain factor of several orders of magnitude in computing time is achieved in specific situations.

The application of equation (1) is restricted to flows, where the mean free path between collisions of molecules is sufficiently large compared to the characteristic length scale of the problem. Some modification of the DSMC method, called Consistent Boltzmann Algorithm, has been developed in the literature, extending the field of application into the direction of moderately dense gases.

In [1] a theoretical foundation for this algorithm was established by deriving the limiting kinetic equation.

This equation generalizes the classical Boltzmann equation (1). A further investigation of its relationship to the Enskog equation was the subject of [2]. First an H-theorem for the new equation was established. Then, following the classical derivation by Chapman and Cowling, approximations to the equations of continuity, momentum, and energy were found. The first order correction terms with respect to the particle diameter turn out to be the same as for the Enskog equation. These results confirm previous derivations, based on the virial, of the corresponding equation of state.

References:

A.L. GARCIA, W. WAGNER, A new kinetic equation for dense gases, in: Rarefied Gas Dynamics, 22nd International Symposium, Sydney, Australia, July 9-14, 2000, T.J. Bartel, M.A. Gallis, eds., chapter 1, volume 585 of AIP Conference Proceedings, AIP Publishing Center, New York, 2001, pp. 17-21.
A. GARCIA, W. WAGNER, Some new properties of the kinetic equation for the consistent Boltzmann algorithm, WIAS Preprint no. 661, 2001.
S. RJASANOW, W. WAGNER, Simulation of rare events by the stochastic weighted particle method for the Boltzmann equation, Math. Comput. Modelling, 33 (2001), pp. 907-926.