Optimization and filtering design

[Next]:

Research Group Interacting Random Systems

[Up]:

Project descriptions

[Previous]:

Parameter estimation in multiphase flow

[Contents]

[Index]

Optimization and filtering design

Collaborator: J. Tseng, V. Schulz

Cooperation with: K.L. Teo (Hong Kong Polytechnic University, China), A. Cantoni (University of Western Australia, Perth), Z. Zang (Australian Telecommunications Research Institute, Perth), R.H.W. Hoppe, S.I. Petrova (Universität Augsburg)

Description:

This project is concerned with the application of optimization techniques to signal processing where the design of a filter can often be cast as a constrained optimization problem. The envelope-constrained (EC) filtering problem is a specific constrained optimization problem. In this problem, we are concerned with the design of a linear time-invariant filter with impulse response u(t) to process a given input signal s(t) which is corrupted by an additive random noise. The objective is to design a filter such that its squared L² norm is minimized, whereas its noiseless output response with respect to a specified input signal stays within a prescribed pulse-shape envelope defined by the lower and upper boundaries. Traditionally, problems of this type were often handled by minimizing the weighted least-mean-square (LMS) difference between the output of the filter and a desired pulse shape. By using output envelope constraints, the EC filtering approach, however, is more relevant than the LMS approach in a variety of signal processing fields such as robust antenna and filter design, radar and sonar detection, and seismology. The continuous-time envelope-constrained filtering problem is then posed as a QP problem with linear inequality constraints:

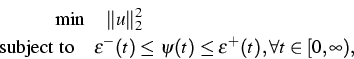
$\begin{eqnarray*} \min\quad\Vert u\Vert^2_2\hspace{4.7cm}\ \mbox{subject to}\qu... ...lon^-(t)\leq\psi(t)\leq\varepsilon^+(t), \forall t\in[0,\infty),\end{eqnarray*}$

where $\psi(t)=\int^\infty_0 u(\tau)s(t-\tau)d\tau$ .Although QP problems have been studied extensively, and a number of efficient optimization algorithms are now available, these algorithms are not suitable for on-line or adaptive applications when the continuous-time domain is substituted by a discrete-time representation. The reason is that their computation requirements at each iteration for the search direction and the corresponding step-size are rather demanding. The goal of this project is to develop an adaptive algorithm based on the gradient flow and space transformation method for solving the filtering problem in a stochastic environment ([1], [2], [3]). Furthermore, we have begun to generalize the methods developed for the solution of linear quadratic programs in this special case to efficient iterative solution techniques for high-dimensional QP subproblems within SQP methods for nonlinear discretized optimization problems.

References:

C.H. TSENG, K.L. TEO, A. CANTONI, Gradient flow approach to discrete-time envelope-constrained filter design via orthonormal filters, IEE Proceedings -- Vision, Image and Signal Processing, 147 (2000), pp. 79-88.
C.H. TSENG, K.L. TEO, A. CANTONI, Z. ZANG, Envelope-constrained filters: Adaptive algorithms, IEEE Trans. Signal Processing, 48 (2000), pp. 1597-1608.
$\dito$ ,Design of robust envelope-constrained filter with orthonormal bases, IEEE Trans. Signal Processing, 48 (2000), pp. 2881-2891.