Optimization problems with random and nonsmooth

[Next]:

Path planning for robots and human

[Up]:

Project descriptions

[Previous]:

Direct and inverse problems in diffractive

[Contents]

[Index]

Optimization problems with random and nonsmooth data

Collaborator: R. Henrion , A. Möller

Cooperation with: W. Römisch (Humboldt-Universität (HU) zu Berlin), G. Wozny (Technische Universität (TU) Berlin), M. Steinbach (Konrad-Zuse-Zentrum für Informationstechnik (ZIB) Berlin), T. Szántai (Technical University of Budapest, Hungary), J. Outrata (Institute of Information Theory and Automation (UTIA) Prague, Czech Republic), A. Jourani (Université de Bourgogne, Dijon, France)

Supported by: DFG: Priority Program ``Echtzeitoptimierung großer Systeme'' (Real-time optimization of large systems)

Description:

The emphasis of this research project is on the solution of applied optimization problems containing random parameters. The analysis of these problems leads to algorithmic challenges and raises new questions about structure and stability.

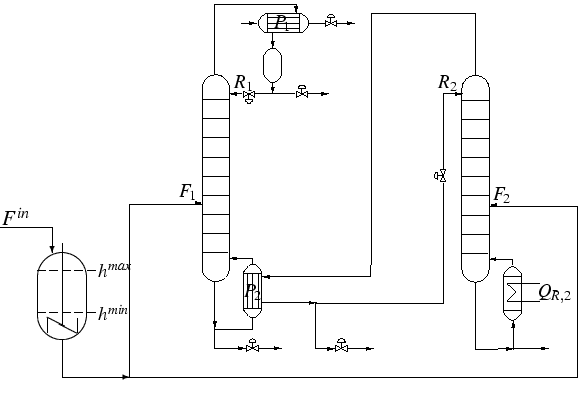
The first application deals with a robust control of a continuous distillation process under random feed conditions. A sketch is given in Fig. 1. This subject has been analyzed in cooperation with G. Wozny (TU Berlin) and co-workers in the framework of a DFG project entitled Real-Time Optimization of Distillation Columns under Probabilistic Constraints (http://www-iam.mathematik.hu-berlin.de/dfg2/ ). The peculiarity here is the need to cope with random parameters given by feed characteristics like inflow rate, composition, and temperature, which are observed only after a decision on the control (feed extraction, heating profile) has been made. The basic approach is a model formulated by means of probabilistic constraints. In previous work, just the inflow rate was assumed to be random. Inside this setting, the focus shifted from rates assumed as a Gaussian process towards rates with an arbitrary deterministic profile affected by random initial time. Numerical results are presented in [1] and [2], whereas structural properties of the arising problems are analyzed in [3] and [4]. Additionally incorporating random composition, however, leads to more complicated structures and requires more sophisticated algorithmic techniques. A first step in this direction has been made by developing (jointly with T. Szántai and J. Bukszár) a method for calculating functional values and gradients of polyhedral chance constraints. The algorithm compares favourably with competing approaches in moderate dimension, but its efficiency has to be improved at dimensions relevant in the application.

A third field of research concerns the investigation of Lipschitz properties of multifunctions arising in general (nonsmooth) optimization problems. Here, an intensive cooperation with J. Outrata (Prague) and A. Jourani (Dijon) shall be continued. The focus of analysis is on subdifferential conditions for the so-called calmness property of constraint mappings which has direct consequences for many important issues of nonlinear optimization like multiplier rules, constraint qualifications, local error bounds, sensitivity or weak sharp minima. First results dealing with Lipschitz data in finite dimensions ([5]) have been extended in [6] to convex data in Banach spaces. The most recent work ([7]) is devoted to more general constraint structures, to applications in complementarity problems, and to the characterization of the stability of solutions. A major challenge to be attacked in the future is the case of Lipschitz data in Banach spaces.

**Fig. 1:** Flow chart of the distillation unit under parallel operation
$%% \ProjektEPSbildNocap {12.85cm}{fb98_4_bild2.eps}$

References:

R. HENRION, A. MÖLLER, Optimization of a continuous distillation process under random inflow rate, to appear in: Comp. Math. Appl.
R. HENRION, P. LI, A. MÖLLER, M. WENDT, G. WOZNY, Optimal control of a continuous distillation process under probabilistic constraints, in: Online Optimization of Large Scale Systems, M. Grötschel et al., eds., Springer, Berlin, 2001, pp. 499-517.
R. HENRION, Structure and stability of probabilistic storage level constraints, to appear in: Proceedings of the 4th GAMM/IFIP Workshop on Stochastic Optimization: Numerical Methods and Technical Applications, K. Marti, ed., LNEMS series, Springer.
$\dito$ , On the connectedness of probabilistic constraint sets, J. Optim. Theory Appl., 112 (2002), pp. 657-663.
R. HENRION, J. OUTRATA, A subdifferential criterion for calmness of multifunctions, J. Math. Anal. Appl., 258 (2001), pp. 110-130.
R. HENRION, A. JOURANI, Boundary-oriented subdifferential characterization of calmness for convex systems, WIAS Preprint no. 645, 2001, to appear in: SIAM J. Optim.
R. HENRION, A. JOURANI, J. OUTRATA, On calmness of a class of multifunctions, WIAS Preprint no. 685, 2001, submitted to: SIAM J. Optim.