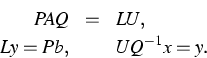Collaborator: J. Borchardt
,
F. Grund
,
D. Horn
Cooperation with: S. Kurz (Robert Bosch GmbH, Stuttgart),
A. Rogowski (EMS Inventa-Fischer, Berlin),
D. Zeitz (Alstom (Switzerland) AG, Baden)
Supported by: Robert Bosch GmbH, Stuttgart
Description:
Over the last three decades, dynamic process simulation has become
an indispensable tool for process design, analysis, and operation in
chemical industry. Due particularly to an improved accuracy of
mathematical process models and an increasing degree of integration in
process modeling, the sizes of the problems which have to be solved
numerically have grown considerably within this time. As a result, the
plantwide dynamic process simulation has become a challenging field
of application for parallel numerical methods.
 For a dynamic process simulation of complex, highly interconnected
plants, initial value problems for large-scale systems of coupled
differential and algebraic equations (DAEs) have to be solved.
Generally, the differential equations arise from balances of energy, mass,
and momentum, while the algebraic relations result from constitutive
relations for phenomenological quantities or different constraints.
These DAE systems are highly nonlinear and can involve several tens of
thousands of equations or even more. Usually their solution components
process at different time scales. The process models depend on
numerous parameters and are often characterized by discontinuities.
For a dynamic process simulation of complex, highly interconnected
plants, initial value problems for large-scale systems of coupled
differential and algebraic equations (DAEs) have to be solved.
Generally, the differential equations arise from balances of energy, mass,
and momentum, while the algebraic relations result from constitutive
relations for phenomenological quantities or different constraints.
These DAE systems are highly nonlinear and can involve several tens of
thousands of equations or even more. Usually their solution components
process at different time scales. The process models depend on
numerous parameters and are often characterized by discontinuities.
Our simulation concept is based on divide-and-conquer techniques and
exploits the hierarchical, modular structure of chemical plants for
large-scale dynamic process simulation on parallel computers. For
that, a plant is considered as a network of connected process units
like reactors, pumps, heat exchangers, or trays of distillation
columns (see Fig. 1). In an equation-based flowsheet
technique, a parameter-dependent mathematical model, describing the
unit operations, is assigned to each unit type, and the units are
connected, e.g., by mass and energy streams. With it, the corresponding
system of DAEs is structured into subsystems according to the units
and can be appropriately partitioned into blocks, which can be treated
almost concurrently. The approach has been implemented in the
Block Oriented Process simulator
BOP that uses its own compiler to
generate a hierarchically structured data interface from a process
description with our modeling language.
In the period under report, we have mainly worked on improving the homogeneous
simulation approach within BOP, in which the entire plant is
modeled by a hierarchically structured, block-partitioned system of
DAEs
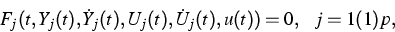
![\begin{displaymath}
F_j :
\mathbb{R}\times\mathbb{R}^{m_j}\times\mathbb{R}^{m_j...
...thbb{R}^{m_j}, ~~~\sum_{i=1}^{p}m_j=n, ~~~t \in
[t_0,t_{end}],\end{displaymath}](../2001/img239.gif)
where the vectors Yj(t) and Uj(t) denote the unknown and coupling
variables of the blocks, respectively, and u(t) the parameter
functions. Within this approach, we use efficiently parallelizable
block-structured Newton-type methods ([1])
to get a widely
applicable parallel approach, covering ``exact'' methods as well as
relaxation techniques. This approach has been improved concerning
block partitioning, an adaptive relaxation decoupling, as well as the
treatment of analytical derivatives for procedures, and a continuation
method has been included into the simulator. With it, the parallel
performance of BOP has been further improved
([2]).
The numerical solution
within BOP requires a repeated solution of
linear systems with the same pattern structure of sparse,
unsymmetric coefficient matrices, and with multiple right-hand sides.
Usually the linear solver requires between 50 and 80 percent of the total
amount of computing time in large-scale applications.
Our direct solver GSPAR is used to solve the linear systemAx = b. It uses advanced direct methods based
on the Gaussian elimination method
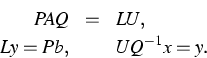
The row permutation matrix P is used to provide numerical stability,
and the column permutation matrix Q is chosen to control sparsity.
In a new approach, at each step of the elimination, the algorithm is
searching for columns with a minimal number of nonzero elements, and a
partial pivoting technique is used to maintain numerical stability.
Table 1:
CPU times (in seconds) for factorization: GSPAR2 compared with
UMFPACK V3
| | GSPAR2 | UMFPACK V3 |
| | First | Second | Symb.+Num. | Redo |
|
Matrix | N | NNZ | Factorization | Factorization | Factorization | Factorization |
| bayer01 |
| lhr34c |
| circuit_4 |
| shermanACb
|
|
| 57 735 |
| 35 152 |
| 80 209 |
| 18 510 |
|
| 277 774 |
| 764 014 |
| 307 604 |
| 145 149 |
|
|
|
| 1.600 |
| 3.133 |
| 950.012 |
| 25.499 |
|
| 0.917 |
| 1.833 |
| 930.063 |
| 23.949 |
|
|
Our new linear solver GSPAR2 has proven to be successful
in simulating several real-life problems. For linear
systems with matrices arising from different technical problems, it
has been compared with the solver UMFPACK V3 (T.A. Davis,
University of Florida, USA) concerning computing time. The results
([5]) are given in Table 1. Here N denotes
the order and NNZ the number of nonzeros of the matrices. The first
two matrices are from chemical process simulation, while the last two
are from circuit simulation. The computations have been performed on a
Compaq AlphaServer GS80 6/731 with 9 GB memory and alpha EV6.7 (21264A)
processors, which operate at 731 MHz.
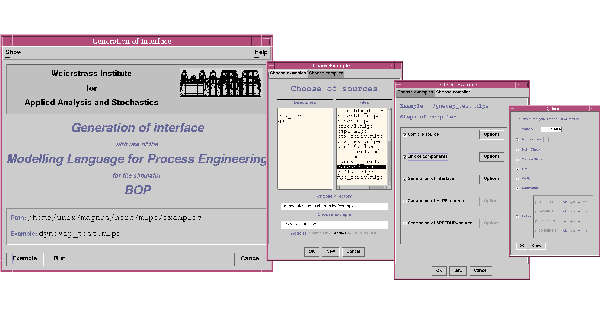
The generation of the data interface for the simulator BOP
consists of three phases that can be controlled separately. To improve
the usage of the compiler, a graphical user interface (GUI) has been
implemented in JAVA. The GUI (see Fig. 2) enables the
selection of examples, the editing of the model and process
description, the selection of different compiler phases, the setting
of compiler parameters, and the evaluation of the resulting data
interface. The compiler itself has been improved regarding the analysis
and treatment of modeling errors.
Fig. 2:
GUI of the modeling language
compiler for the simulator BOP
|
In the period under report, a continuing interest of industrial
partners in our simulation concept has been maintained. The work
concerning the realization of a continuation method within
BOP for solving a special industrial problem has been
successfully finished and was fully financed by the cooperation
partner. Due to the request of another industrial partner, a
PC version of BOP running under WindowsNT is in preparation.
Finally we have started work to adapt a SPICE-like description
language in the area of electric circuit simulation to our process
description language, so that in the future, the simulator BOP
will be applicable to circuit simulation problems as well.
First results concerning an inhomogeneous simulation approach
have been reported in [3], [4].
References:
-
J. BORCHARDT, Newton-type decomposition methods in large-scale
dynamic process simulation , Comput. Chem. Engng., 25
(2001), pp. 951-961.
-
 , Newton-type decomposition methods in parallel
process simulation , in: Proceedings of ICheaP-5,
the 5th Italian Conference on Chemical and Process Engineering,
S. Pierucci, ed., vol. 1, AIDIC, Florence, 2001, pp. 459-464.
, Newton-type decomposition methods in parallel
process simulation , in: Proceedings of ICheaP-5,
the 5th Italian Conference on Chemical and Process Engineering,
S. Pierucci, ed., vol. 1, AIDIC, Florence, 2001, pp. 459-464.
- K. EHRHARDT, J. BORCHARDT, F. GRUND, D. HORN, Distributed
dynamic process simulation , Z. Angew. Math. Mech., 81
(2001), pp. S715-S716.
-
F. GRUND, K. EHRHARDT, J. BORCHARDT, D. HORN, Heterogeneous
dynamic process flowsheet simulation of chemical plants , to appear
in: Mathematics -- Key Technology for the Future II, K.-H. Hoffmann,
W. Jäger, T. Lohmann, H. Schunck, eds., Springer, Berlin.
- F. GRUND, Solution of linear systems
with sparse matrices, talk at the workshop
``Modellierung, Simulation und
Optimierung integrierter Schaltkreise'', November 2001, Mathematisches
Forschungsinstitut Oberwolfach,
(see http://www.wias-berlin.de/~grund/oberwolfach_01.pdf
).
LaTeX typesetting by I. Bremer
9/9/2002
 For a dynamic process simulation of complex, highly interconnected
plants, initial value problems for large-scale systems of coupled
differential and algebraic equations (DAEs) have to be solved.
Generally, the differential equations arise from balances of energy, mass,
and momentum, while the algebraic relations result from constitutive
relations for phenomenological quantities or different constraints.
These DAE systems are highly nonlinear and can involve several tens of
thousands of equations or even more. Usually their solution components
process at different time scales. The process models depend on
numerous parameters and are often characterized by discontinuities.
For a dynamic process simulation of complex, highly interconnected
plants, initial value problems for large-scale systems of coupled
differential and algebraic equations (DAEs) have to be solved.
Generally, the differential equations arise from balances of energy, mass,
and momentum, while the algebraic relations result from constitutive
relations for phenomenological quantities or different constraints.
These DAE systems are highly nonlinear and can involve several tens of
thousands of equations or even more. Usually their solution components
process at different time scales. The process models depend on
numerous parameters and are often characterized by discontinuities.
![\begin{displaymath}
F_j :
\mathbb{R}\times\mathbb{R}^{m_j}\times\mathbb{R}^{m_j...
...thbb{R}^{m_j}, ~~~\sum_{i=1}^{p}m_j=n, ~~~t \in
[t_0,t_{end}],\end{displaymath}](../2001/img239.gif)