[Next]:

Numerical simulation of electro-chemical processes in

[Up]:

Project descriptions

[Previous]:

Numerical aspects of unsteady incompressible non-Newtonian

 [Contents] 

 [Index] 

Convective mechanisms in full-zone liquid bridges

Collaborator: D. Davis  

Cooperation with: F. Smith (University College London, UK)

Description:

This project is chiefly concerned with the numerical investigation of nonlinear, convective mechanisms in liquid bridges of full-zone extent, with an aim to better understand the nature of time-dependent instability for low-Prandtl number (Pr) flows. This is especially pertinent in the field of semiconductor single-crystal growth via the floating-zone method,   where such instabilities are known to be a major cause of striations in crystals ([1], [2]). Of particular importance are the rôles played by buoyancy in the melt region ($\Omega$) and thermocapillarity (Marangoni convection) on the liquid/gas interface ($\Gamma_{LG}$)(see fig1_dd.eps).

The fluid motion and heat transport in $\Omega$ are modeled by the Navier-Stokes equations   with Boussinesq approximation, the incompressibility condition, and the energy equation. The temperature is prescribed on all boundaries (in particular, having an axisymmetric, sinusoidal form on $\Gamma_{LG}$), while the no-slip condition is assumed to hold on the solid/liquid parts ($\Gamma_{SL}$). Also on $\Gamma_{LG}$, a tangential stress condition is applied to account for the Marangoni influence there; the liquid-gas interface is moreover assumed to be non-moving and cylindrical.

A variational form of the equations was chosen which could naturally incorporate the stress boundary condition ([3]); this can be characterized by the treatment of the steady Stokes part of the momentum equation, i.e. its conversion to a ``strain'' form:

$$\int\limits_{\Omega} \{- \Delta \mathbf{u} + \nabla p\} \cdo... ...-\int\limits_{\Gamma_{LG}} \mathbf{n}\cdot\sigma\mathbf{v} ds,$$

where $\mathbf{u}$, p denote velocity and pressure in turn, $\sigma$ is the fluid stress tensor, $\mathbf{n}$ is the unit outer normal to $\Gamma_{LG}$, and $D(\mathbf{u}):=\nabla\mathbf{u} + (\nabla\mathbf{u})^{\rm T}$ is the strain tensor, while $\mathbf{v}$ is an appropriately defined test function.

 

Fig. 1: Sketch of a cylindrical liquid-bridge domain  

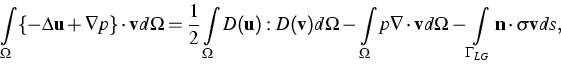
The flow is assumed to be steady and two-dimensional (2-d) axisymmetric, which is valid provided the maximum temperature deviation in the melt is sufficiently small. In particular then, owing to rotational symmetry, the volume integrals that appear in the variational formulation can be reduced to plane integrals, since

$$\int\limits_{\Omega} f d\Omega = 2\pi \int\limits_{S} rf dr dz$$

holds for any continuous function f(r,z) defined in the melt region $\Omega$; here S is a vertical half-plane/cylinder intersection region of arbitrary azimuthal angle (as shown in fig1_dd.eps).

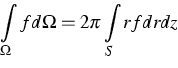
To better understand the possible influences of the underlying convective mechanisms on the flow and thermal development, and therefore be better placed to interpret any subsequent instability features that may emerge, a first study has been made for sub-critical parameter values. Here the relevant parameters are the Rayleigh number (Ra) and the Marangoni number (Ma), with the values Ra/Pr, Ma/Pr indicating the typical sizes of the buoyancy and thermocapillary forces. Their influence relative to one another can be observed in fig2a_dd.eps, for example, where the Prandtl number is 0.01.

 

Fig. 2: Computed velocity field in a domain of unit aspect ratio for (a) pure thermocapillarity ($Ra/Pr=0,\ Ma/Pr=100$); (b) mixed buoyancy-thermocapillarity ($Ra/Pr=100,\ Ma/Pr=10$); (c) pure buoyancy ($Ra/Pr=100,\ Ma/Pr=0$) 

Direct numerical simulations (numerical methodology described below) were performed for low-Prandtl number flows in domains of various aspect ratios, including slender and wide cases, and, allied with nonlinear theory, several nonlinear phenomena could be identified and interpreted ([4]). In particular, for slender domains, this includes a strong convective effect in a box-shaped Euler zone around the mid-horizontal plane of the melt zone, where bell-shaped local velocity profiles, associated with an increased relative Marangoni effect, are seen to emerge. Also high shears are evident in zones (again of Euler type) near the solid boundaries, where the flow turns. fig3a_dd.eps illustrates this effect.

For the spatial discretization of the governing system of equations, a standard Bubnov-Galerkin finite-element method   is applied on 2-d simplicial meshes using globally-continuous, piecewise-quadratic basis functions for the discrete velocity and temperature spaces, and globally-continuous, piecewise-linear basis functions for the discrete pressure space, i.e. the P₂-P₁ (Taylor-Hood triangular) element. The corresponding meshes are generated via new-node bisection from an initial coarse macro-triangulation of the discrete domain S_h.

To discretize in time, a fractional-$\theta$ scheme ([5]) is applied to the hydrodynamic part together with a first-order, semi-implicit, backward-Euler scheme for the energy equation. The principal advantage of the former is the full decoupling of the nonlinearity and incompressibility, which then yields two distinct types of sub-problem: a self-adjoint, quasi-linear, Stokes system for velocity and pressure, and an asymmetric, nonlinear system for velocity only; the first of these is solved by applying a preconditioned conjugated-gradient method ([5]) to the associated Schur-complement equation for pressure, while the second is solved using the GMRES scheme ([6]).

 

Fig. 3: Pure thermocapillary motion in a slender domain (aspect ratio of 0.1) for four cases, depicting axial variations along the mid-vertical line (of the plane S) of (a) the scaled radial velocity component, u_r (b) the scaled axial velocity component, u_z  

References:

1.   C. CUVELIER, J. DRIESSEN, Thermocapillary free boundaries in crystal growth, J. Fluid Mech., 169 (1986), pp. 1-26.
2.   G. MÜLLER, A. OSTROGORSKY, Convection in melt growth, in: Handbook of Crystal Growth 2B, D. Hurle, ed., Elsevier Science, North-Holland, 1994, pp. 709-819.
3.  E. BÄNSCH, Finite element discretization of the Navier-Stokes equations with a free capillary surface, Numer. Math., 88 (2001), pp. 203-235.
4.  D. DAVIS, F. SMITH, Flow and thermal convection in full-zone liquid bridges of wide-ranging aspect ratio, in preparation.
5.  M. BRISTEAU, R. GLOWINSKI, J. PERIAUX, Applications to the simulation of compressible and incompressible flows, Computer Physics Report, 6 (1987), pp. 73-188.
6.  Y. SAAD, M. SCHULZ, GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear equations, SIAM J. Sci. Stat. Comput., 7 (1986), pp. 856-869.

[Next]:

Numerical simulation of electro-chemical processes in

[Up]:

Project descriptions

[Previous]:

Numerical aspects of unsteady incompressible non-Newtonian

 [Contents] 

 [Index]