Long-time dynamics in adaptive gain control

[Next]:

Research Group Numerical Mathematics and Scientific

[Up]:

Project descriptions

[Previous]:

Estimates of the dimension for attractors

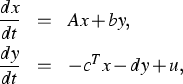
[Contents]

[Index]

Long-time dynamics in adaptive gain control systems

Collaborator: K.R. Schneider

Cooperation with: G.A. Leonov (St. Petersburg University, Russia), A. Ilchmann (Technische Universität Ilmenau)

Description:

We assume that the plant to be controlled can be described by a finite dimensional single input single output linear time invariant system that can be stabilized by a high gain output feedback . Such systems can be represented in the form

$\parbox {13cm}{ \begin{eqnarray*} \frac{dx}{dt} & = & Ax + by, \ \frac{dy}{dt} & = & - c^T x-dy + u,\end{eqnarray*}}$ $% latex2html id marker 3031 \parbox {1cm}{\begin{eqnarray}\end{eqnarray}}$

where u is the input, y the output, $(x,y) \in R^n \times R$ is the state of the system. We apply the adaptive feedback law

$\parbox {13cm}{ \begin{eqnarray*} u & = & -zy +e, \ \frac{dz}{dt} & = & - \sigma z + y^2, \quad z(0) \gt 0,\end{eqnarray*}}$ $% latex2html id marker 3035 \parbox {1cm}{\begin{eqnarray}\end{eqnarray}}$

where e is the control offset error.

Control systems of such type have been investigated, e.g., by I. Mareels et al. [5] and A. Ilchmann [4]. An essential aim of [5] was to show by a bifurcation analysis and by numerical investigations that already in the case n=1 the long-time dynamics of (1), (2) can be very rich, including chaotic behavior. Therefore, from the point of control theory it is desirable to find conditions for (1), (2) to be globally stable or to minimize the region G containing the global attractor.

The goal of the project was to study the long-time dynamics of (1), (2). To this end we constructed an appropriate Lyapunov function. An essential part of this function is some quadratic form defined by means of a symmetric positive definite matrix H. For the existence and also for the construction of H we used frequency domain methods, in particular, we applied some version of the Yakubovich-Kalman frequency domain theorem (see, e.g., [3]).

This way we were able to estimate the global attractor and to derive conditions that (1), (2) were globally asymptotical stable which improve corresponding results in [5].

Using a theorem of Douady-Oesterle ([1]) we were able to estimate the Hausdorff dimension of the global attractor and to derive conditions for the global stability in the case of a vanishing control offset error.

Furthermore, we could establish an upper bound for the Hausdorff dimension of the global attractor.

The results have been presented in [2], a corresponding publication appeared in Lecture Notes in Control and Information Sciences ([6]).

References:

A. DOUADY, J. OESTERLE, Dimension de Hausdorff des attracteurs , C.R. Acad. Sci. Paris Ser. A, 290 (1980), pp. 1135-1138.
G.A. LEONOV, K.R. SCHNEIDER, Longtime dynamics in adaptive gain control systems , WIAS Preprint no. 687 , 2001.
G.A. LEONOV, D.V. PONOMARENKO, V.B. SMIRNOVA, Frequency-domain methods for nonlinear analysis, theory and applications , World Scientific Series on Nonlinear Science, Series A, Vol. 9, 1996.
A. ILCHMANN, Non-identifier-based high-gain adaptive control , Springer, London, 1993.
I. MAREELS, S. VAN GILS, J.W. POLDERMAN, A. ILCHMANN, Asymptotic dynamics in adaptive gain control , in: Advances in Control: Highlights of ECC '99, P.M. Frank, ed., Springer, 1999, pp. 29-63,
G.A. LEONOV, K.R. SCHNEIDER, Longtime dynamics in adaptive gain control systems, in: Dynamics, Bifurcations and Control, F. Colonius, L. Grüne, eds., Lecture Notes in Control and Information Sciences, Vol. 273, Springer, Berlin, 2002, pp. 241-254.