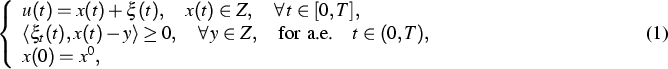
where
where
|
|
|
[Contents] | [Index] |
Cooperation with: N. Kenmochi (Chiba University, Japan), P. Krejcí (Academy of Sciences of the Czech Republic, Prague), U. Stefanelli (Università di Pavia, Italy), C. Verdi (Università di Milano, Italy), S. Zheng (Fudan University, Shanghai, China)
Supported by: DFG: ``Hysterese-Operatoren in Phasenfeld-Gleichungen'' (Hysteresis operators in phase-field equations)
Description:
To be able to deal with phase transitions, one has to take into account diffusive effects as well as hysteretic phenomena.
(a)
The hysteretic phenomena are modeled by hysteresis operators.
A typical example is the
multi-dimensional stop operator ![]() with the characteristic set Z ,
which is defined for a convex, closed subset Z of
with the characteristic set Z ,
which is defined for a convex, closed subset Z of ![]() .For a final time T > 0,
this operator maps a pair (u,x0) consisting of an
input function
.For a final time T > 0,
this operator maps a pair (u,x0) consisting of an
input function ![]() and some
and some ![]() to the
solution
to the
solution ![]() to the variational inequality
to the variational inequality
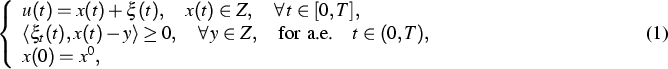
where ![]() denotes the inner product on
denotes the inner product on
![]() .The stop operator is used to define the corresponding
multi-dimensional Prandtl-Ishlinskii operators
.The stop operator is used to define the corresponding
multi-dimensional Prandtl-Ishlinskii operators
![]()
where ![]() is a real-valued function and, for
is a real-valued function and, for ![]() ,
,![]() is an initial value for the stop operator SrZ
with the characteristic set rZ.
In [9],
these hysteresis operators are investigated, and for
a phase-field system
involving multi-dimensional Prandtl-Ishlinskii operators
the existence of a unique solution is proved. This is an
extension of results in the previous work ([8]),
since it is no longer required
that the domain Z must be polyhedral.
More general classes of multi-dimensional Prandtl-Ishlinskii operators
have been studied in [11].
is an initial value for the stop operator SrZ
with the characteristic set rZ.
In [9],
these hysteresis operators are investigated, and for
a phase-field system
involving multi-dimensional Prandtl-Ishlinskii operators
the existence of a unique solution is proved. This is an
extension of results in the previous work ([8]),
since it is no longer required
that the domain Z must be polyhedral.
More general classes of multi-dimensional Prandtl-Ishlinskii operators
have been studied in [11].
The mathematical modeling of nonlinear thermo-visco-plastic
developments leads to the following system
![\begin{gather}
\rho u_{tt} - \mu u_{xxt} = \sigma_x + f(x,t),
\ \sigma = {\math...
... \nu w_t + {\mathcal H}_3[u_x,w] + \theta {\mathcal H}_4[u_x,w] = 0,\end{gather}](../2001/img106.gif)
where u, ![]() ,
, ![]() , and w are the unknowns
displacement, absolute temperature, elastoplastic stress, and
freezing index, respectively,
, and w are the unknowns
displacement, absolute temperature, elastoplastic stress, and
freezing index, respectively,
![]() ,
, ![]() , CV, and
, CV, and ![]() are positive constants,
f, g are given functions,
and
are positive constants,
f, g are given functions,
and
![]() , and
, and ![]() are
hysteresis operators.
In [12], this system has been derived,
the thermodynamic consistency of the model has been proved,
and the existence of a unique strong solution
to an initial-boundary value problem for this system has been shown. A
large time asymptotic result for this system is presented in
[5].
For almost the same problem with a more general boundary condition,
similar existence and asymptotic results
have been derived.
An approach used in [5] to derive uniform estimates for the solutions
to partial differential equations involving hysteresis operators
has been further investigated in [6].
Moreover, in [6],
generalizations of the scalar Prandtl-Ishlinskii operators
are introduced and
investigated with respect to their thermodynamic consistency.
are
hysteresis operators.
In [12], this system has been derived,
the thermodynamic consistency of the model has been proved,
and the existence of a unique strong solution
to an initial-boundary value problem for this system has been shown. A
large time asymptotic result for this system is presented in
[5].
For almost the same problem with a more general boundary condition,
similar existence and asymptotic results
have been derived.
An approach used in [5] to derive uniform estimates for the solutions
to partial differential equations involving hysteresis operators
has been further investigated in [6].
Moreover, in [6],
generalizations of the scalar Prandtl-Ishlinskii operators
are introduced and
investigated with respect to their thermodynamic consistency.
The system (3)-(6) can be simplified by adding uxxxx on the left-hand side of (3). The corresponding system has been considered in [13].
(b)
Phase-field systems of Penrose-Fife type are models for diffusive
phase-transition phenomena, see [14].
For a non-conserved scalar order parameter ![]() , one
gets the system
, one
gets the system
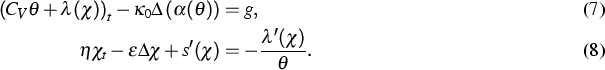
In this system CV, ![]() , and
, and ![]() are given positive constants,
and
are given positive constants,
and ![]() ,
, ![]() , s, g are given functions.
, s, g are given functions.
In [7], an a posteriori error estimate
has been derived for a time-discrete scheme for
the system
(7)-(8),
with
![]() being a positive constant, and
being a positive constant, and ![]() .
.
The system
(7)-(8)
with ![]() depending on
depending on ![]() can be used to model the anisotropic
solidification of liquids. The existence of a solution to this
system has been shown in [4].
can be used to model the anisotropic
solidification of liquids. The existence of a solution to this
system has been shown in [4].
Following [1, 2],
the system (7)-(8)
is modified by replacing ![]() in (8)
by an integral
operator and allowing
in (8)
by an integral
operator and allowing ![]() to be a function of
to be a function of ![]() .
For an integrodifferential (non-local) system
derived in this way, results concerning global existence, uniqueness, and
large-time asymptotic behavior have been derived in
[15].
.
For an integrodifferential (non-local) system
derived in this way, results concerning global existence, uniqueness, and
large-time asymptotic behavior have been derived in
[15].
In another modification of the phase-field system,
the energy balance
(7) is coupled with two order parameter
equations:
![]()
where w is a scalar-valued order parameter,
![]() is an order parameter with values in
is an order parameter with values in ![]() ,and
,and
![]() is the subdifferential of the indicator function
IZ of a bounded, closed, convex set
is the subdifferential of the indicator function
IZ of a bounded, closed, convex set ![]() .Formally, this system can be considered as a diffusive approximation of the
corresponding multi-dimensional stop operator
.Formally, this system can be considered as a diffusive approximation of the
corresponding multi-dimensional stop operator ![]() .Results concerning existence, uniqueness, and continuous dependence on data
have been presented in [3].
.Results concerning existence, uniqueness, and continuous dependence on data
have been presented in [3].
In [10], it has been proved for another phase-field system that the solutions are approximations for the evaluation of the stop operator.
References:
|
|
|
[Contents] | [Index] |