Collaborator: H. Gajewski
,
K. Zacharias
Description:
We consider a binary alloy with components 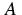 and
and 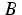 occupying a spatial domain
occupying a spatial domain 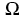 . We denote by
. We denote by 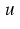 and
and 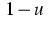 the (scaled) local concentrations of
the (scaled) local concentrations of 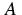 and
and 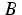 , respectively.
Let
, respectively.
Let 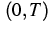 denote a time interval,
denote a time interval, 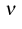 the outer unit
normal on the boundary
the outer unit
normal on the boundary 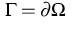 , and
, and 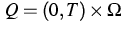 ,
,
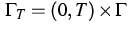 .
.
To describe phase separation in
binary systems, one usually uses the Cahn-Hilliard equation. This
equation is derived
([1])
from a free energy functional of the form
| 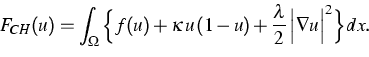 |
(1) |
Here 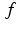 is a convex function with the property that
is a convex function with the property that
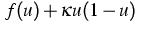 (for sufficiently large
(for sufficiently large 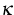 )
forms a so-called
double well potential. Minimizing FCH under the constraint of mass
conservation,
one identifies the Lagrange multiplier v via the associated
Euler-Lagrange equation
)
forms a so-called
double well potential. Minimizing FCH under the constraint of mass
conservation,
one identifies the Lagrange multiplier v via the associated
Euler-Lagrange equation
| 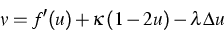 |
(2) |
as chemical potential.
Now one postulates that 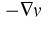 is the driving force for the
mass flux
is the driving force for the
mass flux 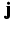 , i.e.
, i.e.
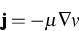
with a suitable mobility 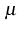 . Considering the mass balance, one
ends up with the Cahn-Hilliard equation
. Considering the mass balance, one
ends up with the Cahn-Hilliard equation
| 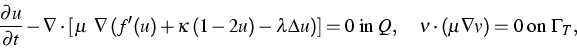 |
(3) |
where the Neumann boundary condition guarantees mass conservation
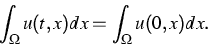
Inspecting Cahn-Hilliard's arguments
([1])
establishing (1)
as the free energy of the binary system, it seems to be reasonable and
even more adequate ([7]) to choose
an alternative nonlocal expression like
| 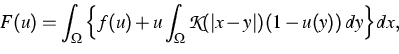 |
(4) |
where the kernel 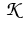 of the integral term describes nonlocal
interaction.
By a simple calculation, we find from (4) the corresponding chemical
potential
of the integral term describes nonlocal
interaction.
By a simple calculation, we find from (4) the corresponding chemical
potential 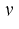 as the gradient of
as the gradient of 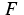 in the form
in the form
| 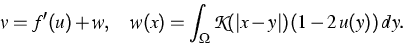 |
(5) |
Replacing (2) by (5), one gets instead of (3) the problem
| 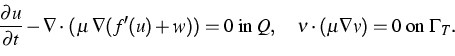 |
(6) |
In the standard case 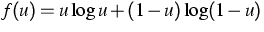 , we have
, we have
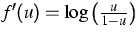 , and hence by (5)
, and hence by (5)
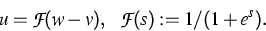
The image of the Fermi function 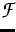 is the interval
is the interval
![$\;[0,1]\;$](../2001/img55.gif) , so that the nonlocal model automatically satisfies the
physical requirement
, so that the nonlocal model automatically satisfies the
physical requirement 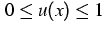 . This property cannot be
guaranteed for solutions of the original Cahn-Hilliard equation, since
for fourth-order equations no maximum principle is available.
Moreover, by physical reasons it is desirable to admit mobilities
. This property cannot be
guaranteed for solutions of the original Cahn-Hilliard equation, since
for fourth-order equations no maximum principle is available.
Moreover, by physical reasons it is desirable to admit mobilities
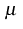 depending on
depending on 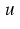 and
and 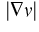 . A natural choice
is
. A natural choice
is 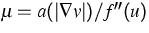 ([2], [7])
with a function
([2], [7])
with a function 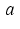 such that
such that 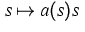 is
monotone. Then
problem (6) can be rewritten as
is
monotone. Then
problem (6) can be rewritten as
| ![\begin{displaymath}
\dfrac{\partial u}{\partial t} -
\nabla \cdot \bigg [a \lef...
...c{\nabla w}{f''(u)} \right)\bigg] = 0
\;\text{on}\; \Gamma_T. \end{displaymath}](../2001/img62.gif) |
(7) |
It seems worth mentioning that diffusion equations with a nonlocal drift term
of this
form also model transport processes in semiconductor ([4]) and
chemotaxis ([5]) theory.
In this project we proved existence and uniqueness of a global solution u
to (7). Moreover, we studied
the asymptotic behavior as time going to infinity and characterized the
asymptotic state by a variational principle ([6]). An extension to
non-isothermal situations was also given ([3]).
References:
- J.C. CAHN, J.E. HILLIARD, Free energy of a
nonuniform system. I. Interfacial free energy, J.
Chem. Phys., 28 (1958), pp. 258-267.
- C.M. ELLIOT, H. GARCKE, On the Cahn-Hilliard
equation with degenerate mobility, SIAM J. Math. Anal., 27
(1996), pp. 404-423.
- H. GAJEWSKI, On a nonlocal model of
non-isothermal phase separation, WIAS Preprint no. 671, 2001, to
appear in: Adv. Math. Sci. Appl.
- H. GAJEWSKI, K. GRÖGER, Semiconductor equations
for variable mobilities based on Boltzmann statistics or
Fermi-Dirac statistics, Math. Nachr., 140 (1989), pp. 7-36.
- H. GAJEWSKI, K. ZACHARIAS, Global behaviour of a
reaction-diffusion system modelling chemotaxis, Math. Nachr.,
195 (1998), pp. 77-114.
-
 , On a nonlocal phase separation
model, WIAS Preprint no. 656, 2001, to appear in: J. Math. Anal. Appl.
, On a nonlocal phase separation
model, WIAS Preprint no. 656, 2001, to appear in: J. Math. Anal. Appl.
- G. GIACOMIN, J.L. LEBOWITZ, Phase segregation
dynamics in particle systems with long range
interactions I. Macroscopic limits, J. Statist. Phys., 87
(1997), pp. 37-61.
LaTeX typesetting by I. Bremer
9/9/2002
![]() and
and ![]() occupying a spatial domain
occupying a spatial domain ![]() . We denote by
. We denote by ![]() and
and ![]() the (scaled) local concentrations of
the (scaled) local concentrations of ![]() and
and ![]() , respectively.
Let
, respectively.
Let ![]() denote a time interval,
denote a time interval, ![]() the outer unit
normal on the boundary
the outer unit
normal on the boundary ![]() , and
, and ![]() ,
,
![]() .
.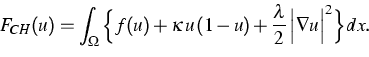
![]()
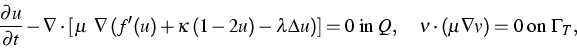
![]()
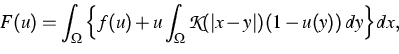
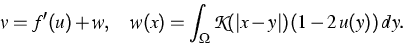
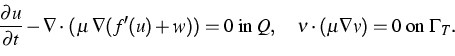
![]()
![\begin{displaymath}
\dfrac{\partial u}{\partial t} -
\nabla \cdot \bigg [a \lef...
...c{\nabla w}{f''(u)} \right)\bigg] = 0
\;\text{on}\; \Gamma_T. \end{displaymath}](../2001/img62.gif)