|
|
|
[Contents] | [Index] |
Kooperation: I. Edelman (Stipendiatin der Alexander von Humboldt-Stiftung, derzeit WIAS), E. Radkevich (Staatliche Universität Moskau, Russland), D. Kolymbas (Universität Innsbruck, Institut für Geotechnik und Tunnelbau)
Beschreibung der Forschungsarbeit:
In Bezug auf Ergebnisse für Schallwellen, die in den letzten Jahren für das eigene Modell für poröse Körper erzielt worden sind, wurden zwei Gebiete der Wellenausbreitung untersucht, nämlich
Für Oberflächenwellen wurden zwei Teilaufgaben gelöst:
Die erste Aufgabe führt für kurze Wellen zu der folgenden
dimensionslosen Dispersionsgleichung (![]()
![\begin{displaymath}
-\frac{i\mu }{2\gamma _{1}\gamma _{2}}\left[ -\left( \rho _{...
...{2}^{S2}}-4\mu \frac{\gamma _{1}\gamma _{2}}{k^{2}}\right] =0, \end{displaymath}](../1999/img447.gif)
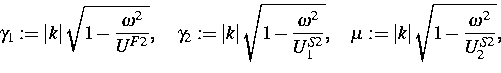
wo U1S,U2S,UF die dimensionslosen
Ausbreitungsgeschwindigkeiten der P1-, S-, P2-Schallwellen bezeichnen, ![]() sind Referenzmassendichten der beiden Komponenten,
sind Referenzmassendichten der beiden Komponenten, ![]() ist die dimensionslose Wellenfrequenz und k die
Wellenzahl. Die asymptotische Analyse dieser Gleichung zeigt, dass
sich zwei Arten von Oberflächenwellen ausbreiten: eine
generalisierte Rayleigh-Welle , die durch Energieübertragung auf
andere Wellen gedämpft ist und deren Geschwindigkeit größer als die
Geschwindigkeit der P2-Wellen ist, und eine
Stoneley-Welle , die die kleinste
Ausbreitungsgeschwindigkeit besitzt und nicht gedämpft ist.
ist die dimensionslose Wellenfrequenz und k die
Wellenzahl. Die asymptotische Analyse dieser Gleichung zeigt, dass
sich zwei Arten von Oberflächenwellen ausbreiten: eine
generalisierte Rayleigh-Welle , die durch Energieübertragung auf
andere Wellen gedämpft ist und deren Geschwindigkeit größer als die
Geschwindigkeit der P2-Wellen ist, und eine
Stoneley-Welle , die die kleinste
Ausbreitungsgeschwindigkeit besitzt und nicht gedämpft ist.
Die zweite Aufgabe basiert auf der Randbedingung für durchlässige
Ränder, die in der Gruppe früher entwickelt worden ist. Es wurde
bewiesen (![]() ), dass in diesem Fall drei Oberflächenwellen
möglich sind: außer zwei Arten, die für einen undurchlässigen
Rand existieren, entsteht eine neue
Pseudo-Stoneley-Welle . Diese Welle wird
gedämpft und breitet sich mit einer Geschwindigkeit aus, die,
ähnlich wie bei der Rayleigh-Welle, etwas größer ist als die
Geschwindigkeit der P2-Welle . Die Eigenschaften dieser
Wellen sind sehr stark vom Oberflächendurchlässigkeitsparameter
), dass in diesem Fall drei Oberflächenwellen
möglich sind: außer zwei Arten, die für einen undurchlässigen
Rand existieren, entsteht eine neue
Pseudo-Stoneley-Welle . Diese Welle wird
gedämpft und breitet sich mit einer Geschwindigkeit aus, die,
ähnlich wie bei der Rayleigh-Welle, etwas größer ist als die
Geschwindigkeit der P2-Welle . Die Eigenschaften dieser
Wellen sind sehr stark vom Oberflächendurchlässigkeitsparameter ![]() abhängig. Diese Arbeit wird im nächsten Jahr fortgesetzt. Es sollen
numerische Beispiele untersucht und Oberflächenwellen auf den
Kontaktflächen zweier verschiedener poröser Körper beschrieben
werden. Außerdem wird versucht, die Ergebnisse praktisch im Bereich der
Bodenmechanik umzusetzen.
abhängig. Diese Arbeit wird im nächsten Jahr fortgesetzt. Es sollen
numerische Beispiele untersucht und Oberflächenwellen auf den
Kontaktflächen zweier verschiedener poröser Körper beschrieben
werden. Außerdem wird versucht, die Ergebnisse praktisch im Bereich der
Bodenmechanik umzusetzen.
Dieses Projekt wird mit Hilfe eines linearisierten Modells
durchgeführt, was für die Beschreibung von Oberflächenwellen
völlig ausreichend ist. Das zweite Forschungsprojekt betrifft die
Ausbreitung von starken Singularitäten, deren Existenz nichtlineare
Beiträge im Modell verlangt. Für diese Aufgabe wurden erste
Ergebnisse mit Hilfe von asymptotischen Methoden erzielt ([3]).
Zum Beispiel wurde gezeigt, dass die Porositätsgleichung, die in dem
eigenen Modell ein wesentlicher Beitrag ist, keine zusätzlichen
Randbedingungen verlangt. Für kinkähnliche Geschwindigkeitswellen
entstehen Pseudosolitonen für die dynamische Störung der
Porosität. Diese Eigenschaft ist charakteristisch für Gleichungen
mit Dispersion, wie zum Beispiel in der Korteweg-de-Vries-Gleichung.
Pseudosolitonen degenerieren zu Dirac-![]() -Singularitäten in der
Null-Grenze des kleinen Parameters
-Singularitäten in der
Null-Grenze des kleinen Parameters ![]() (dynamische Kopplung der
Komponenten).
(dynamische Kopplung der
Komponenten).
Projektliteratur:
|
|
|
[Contents] | [Index] |