Bearbeiter: J. Fuhrmann
(FG 3),
H. Langmach
(FG 3),
K. Gärtner
(FG 7)
Beschreibung der Forschungsarbeit:
Auf der Grundlage der Perron-Frobenius-Theorie nichtnegativer Matrizen
konnten neue Resultate zur Existenz und Einzigkeit von Lösungen
nichtlinearer Gleichungssysteme mit außerdiagonaler Nichtlinearität
erzielt werden. Diese Ergebnisse lassen sich auf zeitimplizite
Finite-Volumen-Diskretisierungen von skalaren nichtlinearen
Erhaltungsgleichungen der Art
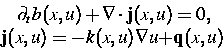
mit stückweise konstanten Ortsabhängigkeiten anwenden. Weiterhin
lassen sich mit Hilfe dieser Methode Aussagen zu Stabilität und
Maximumprinzipien für die diskreten Gleichungen ableiten.
Anwendungen dieser Resultate finden sich beim gesättigt/ungesättigten
Fluidtransport
und bei
nichtlinearen Wärmeleitprozessen.
Auf der Grundlage struktureller Überlegungen zur Darstellung der
diskreten nichtlinearen Operatoren ist es möglich, die numerischen
Verfahren auf Systeme vom Typ
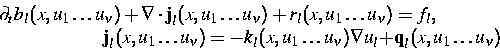
aus k Gleichungen in ein-, zwei- und dreidimensionalen Gebieten zu
verallgemeinern. Der entsprechende Code -
pdelib/sysconlaw
-
ist inzwischen Ausgangspunkt
für die Anwendungsprojekte
,,Simulation des gekoppelten Wärme- und Fluidtransports`` und
,,Zweiphasenströmungen in porösen Medien``.
Abb. 1:
Stabile (links) und instabile (rechts) Diskretisierung des
gesättigt/ungesättigten Grundwasserflusses
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.3\textwidth}{fv-1.eps}{fv-2.eps}
\makeatother](../../1998/html/images/img418.gif) |
Projektliteratur:
- J. FUHRMANN, Existence and uniqueness of solutions of certain
systems of algebraic equations with off diagonal nonlinearity,
WIAS-Preprint No. 425, 1998.
- J. FUHRMANN, H. LANGMACH, Stability of solutions of
time-implicit finite volume schemes for viscous nonlinear conservation laws,
WIAS-Preprint No. 437, 1998.
LaTeX typesetting by I. Bremer
7/30/1999
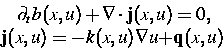
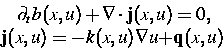
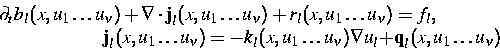
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.3\textwidth}{fv-1.eps}{fv-2.eps}
\makeatother](../../1998/html/images/img418.gif)