Approximation und Optimierung von Platten

[Next]:

Gekoppelter Fluid- und Wärmetransport

[Up]:

Projektbeschreibungen

[Previous]:

Modellierung, Analyse und Simulation des Widerstands-Impulsschweißens

[Contents]

[Index]

Approximation und Optimierung von Platten

Bearbeiter: H. Langmach (FG 3), J. Sprekels (FG 1)

Kooperation: V. Arnautu (Universität Iasi, Fachbereich für Mathematik), D. Tiba (Rumänische Akademie der Wissenschaften, Bukarest)

Beschreibung der Forschungsarbeit: Die Auslenkung $\,y = y\, (x_1, x_2)\,$ einer dünnen Platte unter der Kraft $\,f = f\, (x_1, x_2)\,$ wird beschrieben durch eine Randwertaufgabe zur biharmonischen Gleichung

$\begin{displaymath} \Delta (u^3\, \Delta y)\,=\,f \quad \mbox{in } \Omega\,\subset\,\IR^2\,,\end{displaymath}$ (30)

wobei $\,u = u\, (x_1, x_2)\,$ die Dicke der Platte bedeutet. Als Randbedingung treten die folgenden Fälle auf:

$\begin{displaymath} y\,=\,\Delta y\,=\,0 \quad\mbox{auf } \partial \Omega\quad \mbox{(gest\uml {u}tzte Platte)}\,,\end{displaymath}$ (31)

$\begin{displaymath} y\,=\,\frac{\partial y}{\partial n}\,=\,0 \quad \mbox{auf } \partial \Omega \quad \mbox{(eingespannte Platte)}\,,\end{displaymath}$ (32)

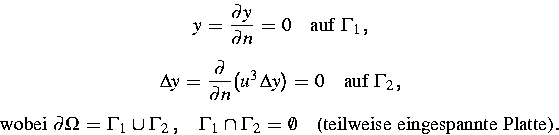
$\begin{eqnarray} &y\,=\,{\displaystyle \frac{\partial y}{\partial n}}\,=\,0 \qua... ...a_2\,=\,\emptyset \quad \mbox{(teilweise eingespannte Platte)}\,.&\end{eqnarray}$

In den früheren Arbeiten [1-3] wurde eine neue Methode zur Approximation und Optimierung von Stäben und Platten entwickelt, die auf einer Dekomposition der Randwertaufgaben (1)+(2) bzw. (1)+(3) in zwei elliptische Randwertprobleme zweiter Ordnung beruht, die als Nebenbedingungen in ein Problem der optimalen Steuerung eingehen. Dabei wurde die Einhaltung der Randbedingungen mittels eines Penalty-Terms im Zielfunktional erzwungen. Neben der Randwertaufgabe wurde auch eine daraus abgeleitete Variationsungleichung behandelt. Die Konvergenz der Penalty-Methoden konnte jeweils gezeigt werden.

Im Berichtsjahr konnten die bisher erzielten Ergebnisse erheblich verbessert werden. So gelang es in [4], für den Fall (1)+(2) der gestützten Platte ein verallgemeinertes Bang-Bang-Prinzip für die optimalen Steuerungen zu beweisen; ferner konnte in [5] erstmalig der schwierige Fall (1)+(4) einer nur teilweise eingespannten Platte unter punktweisen Zustandsrestriktionen behandelt werden. Dabei gelang der Nachweis der Konvergenz für das verwendete Penalty-Verfahren, und für die approximativen Lösungen konnten die Eindeutigkeit nachgewiesen sowie die notwendigen Optimalitätsbedingungen hergeleitet werden.

In numerischer Hinsicht hat der gewählte Zugang den Vorteil, daß bei der Problemlösung stückweise lineare finite Elemente verwendet werden können und keine Elemente höherer Ordnung benötigt werden.

Projektliteratur:

V. ARNAUTU, H. LANGMACH, J. SPREKELS, D. TIBA, On the approximation and optimization of plates, WIAS-Preprint No. 357 , 1997, eingereicht.
J. SPREKELS, D. TIBA, A duality-type method for the design of beams, WIAS-Preprint No. 222 , 1996, erscheint in: Adv. Math. Sci. Appl.
$\dito$ , A duality approach in the optimization of beams and plates, WIAS-Preprint No. 335 , 1997, erscheint in: SIAM J. Control Optimiz.
$\dito$ , Propriétés de bang-bang généralisées dans l'optimisation des plaques, C. R. Acad. Sci. Paris, Ser. I, t. 327 (1998), pp. 705-710.
$\dito$ , On the approximation and optimization of fourth order elliptic systems, erscheint in: Proceedings der IFIP-Tagung 1998 in Chemnitz.