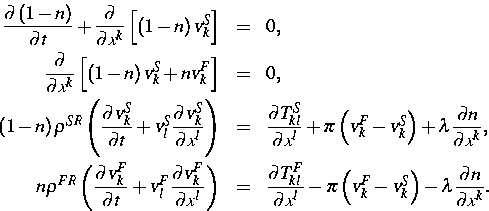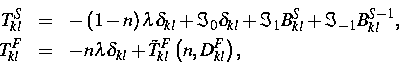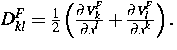Modellbildung poröser und granularer Stoffe

[Next]:

Gruppenübergreifende Projekte

[Up]:

Projektbeschreibungen

[Previous]:

Martensitische Umwandlung

[Contents]

[Index]

Modellbildung poröser und granularer Stoffe

Bearbeiter: K. Wilmanski

Kooperation: T. Ruggeri (Universität Bologna), K. Hutter (Technische Universität Darmstadt), W. Wendland (Universität Stuttgart)

Beschreibung der Forschungsarbeit: Die Fortsetzung der Modellbildung für poröse und granulare Stoffe geschieht aus drei Gründen:

Anpassung der Struktur des Modells an die Struktur der erweiterten Thermodynamik,
Untersuchung der Einbettung des eigenen Modells in die Klasse der kontinuumsthermodynamischen Modelle für poröse und granulare Stoffe, insbesondere die Klasse der Modelle mit höheren Gradienten und Inkompressibilitätsannahmen,
Vorbereitung der kinetischen und makroskopischen Modellbildung für granulare Stoffe mit hierarchischer Struktur der Transfergleichungen.

Die erste Aufgabe wurde in diesem Jahr abgeschlossen [1]. Es wurde gezeigt, daß die eigene Lagrangesche Modellbildung die Darstellung der hyperbolischen Feldgleichungen wesentlich vereinfacht und eine Erweiterung auf nichtisotherme Vorgänge ermöglicht. Diese Arbeit liegt auch der Untersuchung der Stoßwellen in porösen und granularen Stoffen zugrunde, die im Jahr 1999 intensiv fortgesetzt wird.

Vor einigen Jahren wurde die Frage nach Inkompressibilität oder allgemeiner nach Zwangsbedingungen in mehrkomponentigen Körpern gestellt [2]. Es wurde gezeigt, daß die üblichen Modelle über mehrkomponentige Körper thermodynamisch nicht zulässig sind. Eine neue Untersuchung hat bewiesen, daß manche Fälle der Modellbildung mit höheren Gradienten die thermodynamische Zulässigkeit doch gewährleisten. 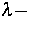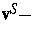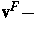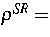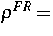Zum Beispiel genügt das Modell mit den Feldern $\lambda -$ Porendruck, n - Porosität, $\mathbf{v}^{S}-$ Geschwindigkeit des Skeletts, $\mathbf{v}^{F}-$ Geschwindigkeit der Flüssigkeit und Feldgleichungen ( $\rho ^{SR}=$ konst., $\rho ^{FR}=$ konst. - Inkompressibilität!)

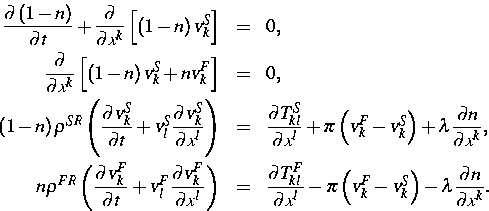
$\begin{eqnarray*} \frac{\partial \left( 1-n\right) }{\partial t}+\frac{\partial ... ...sl v}_{k}^{S}\right) -\lambda \frac{\partial n}{\partial x^{k}}.\end{eqnarray*}$

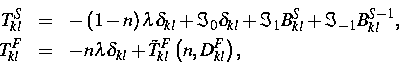
$\begin{eqnarray*} T_{kl}^{S} &=&-\left( 1-n\right) \lambda \delta _{kl}+\Im _{0}... ...ambda \delta _{kl}+\tilde{T}_{kl}^{F}\left( n,D_{kl}^{F}\right),\end{eqnarray*}$

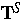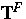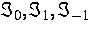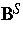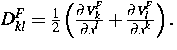
dem zweiten Hauptsatz [3]. In diesen Gleichungen sind $\mathbf{T}^{S}$ und $\mathbf{T}^{F}$ partielle Spannungstensoren, $\Im _{0},\Im _{1},\Im _{-1}$ - Elastizitätskoeffizienten (abhängig von der Verzerrung des Skeletts $\mathbf{B}_{{}}^{S}$ und der Porosität) und $D_{kl}^{F}=\frac{1}{2}\left( \frac{\partial \mbox{\sl v}_{k}^{F}}{\partial x^{l}}+\frac{\partial \mbox{\sl v}_{l}^{F}}{\partial x^{k}}\right).$

Dieses Modell beschreibt Sedimentationsvorgänge und wird mathematisch von der Forschungsgruppe von Prof. W. Wendland (Stuttgart) untersucht.

Neue Elemente der Modellbildung stehen in engem Zusammenhang mit dem Forschungsvorhaben für 1999. Es sollen nämlich kinetische Grundlagen der Theorie der granularen Stoffe erforscht werden mit dem Ziel, Transfergleichungen mit Hilfe des Prinzips der Maximalen Entropie zu bilden. Auf diesem Gebiet hat die Forschungsgruppe schon umfangreiche Vorarbeiten geleistet.

Projektliteratur:

K. WILMANSKI, Toward an extended thermodynamics of porous and granular materials, erscheint in: Proceedings of STAMM '98, Nice, (1999).
$\dito$ , On incompressibility of true components in porous materials, in: Festschrift zum 60. Geburtstag von Prof. Dr. Reint de Boer, Forschungsberichte FB Bauwesen, No. 66, Universität Essen, 1995.
$\dito$ , Note on the notion of incompressibility in theories of porous and granular materials, WIAS-Preprint No. 465, 1998.