Simulation dynamischer Prozesse in chemischen Anlagen

Kooperation: St. Artlich, F. Hubbuch (Bayer AG, Leverkusen), P. Capek (Akademie der Wissenschaften der Tschechischen Republik, Prag), M. Häfele, M. Mangold (Max-Planck-Institut für Dynamik komplexer technischer Systeme, Magdeburg), A. R. Rodríguez S. (Humboldt-Universität zu Berlin)

Beschreibung der Forschungsarbeit: Die mathematische Modellierung der verfahrenstechnischen Prozesse, die in Produktionsanlagen der chemischen Industrie ablaufen, führt im allgemeinen auf Anfangswertprobleme für große Systeme von nichtlinearen Algebro-Differentialgleichungen (DAE). Um den Anforderungen unserer Kooperationspartner bei der dynamischen Simulation gesamter Anlagen unter Verwendung immer komplexerer Modelle gerecht werden zu können, ist der Einsatz effizienter numerischer Verfahren zur Lösung der DAE-Systeme auf Parallelrechnern erforderlich. Die von uns hierfür verwendeten Simulationsansätze nutzen die durch die Modellierung vorgegebene hierarchische Struktur der Anlagen für die Parallelisierung mit diakoptischen Methoden aus. Dabei wird die Anlage als ein Netzwerk von Prozeßeinheiten (Units) beschrieben, die durch Stoff- und Wärmeströme miteinander gekoppelt sind. Die entstehenden DAE-Systeme sind entsprechend dieser Units in m Teilsysteme strukturiert

$\begin{displaymath} F_i : \mathbb{R}\times\mathbb{R}^n\times\mathbb{R}^n\times... ...thbb{R}^{n_i}, ~~~\sum_{i=1}^{m}n_i=n, ~~~t \in [t_0,t_{end}],\end{displaymath}$

Basierend auf dieser Teilsystemstruktur werden die DAE-Systeme in Blöcke partitioniert. Eine solche Partitionierung kann vorgegeben oder durch Partitionierungsalgorithmen generiert werden. Durch geeignete Erweiterung der bei der Verwendung von BDF-Verfahren in jedem Diskretisierungszeitpunkt entstehenden nichtlinearen Gleichungssysteme können diese durch effektiv parallelisierbare blockstrukturierte Verfahren vom Newton-Typ (BSN) gelöst werden. Diese Verfahren basieren auf einem Block-Schurkomplement-Ansatz und ermöglichen den Einsatz sowohl von Multilevel-Iterations- als auch von adaptiven Relaxations-Techniken [1]. Die Verfahren sind im Prototyp unseres dynamischen Prozeßsimulators BOP (Block Oriented Process simulator) integriert. Der Simulator ist auf Parallelrechnern mit Shared Memory vom Typ Cray J90 und SGI Origin 2000 implementiert und hat sich bei Simulationsrechnungen für komplexe Anlagen der Bayer AG, Leverkusen, bewährt.

Ein neuer Typ von blockstrukturierten Newton-Verfahren [2] (im weiteren Verfahren vom Typ 2 genannt) basiert auf der Kennzeichnung der Koppelvariablen zwischen Blöcken als Eingangs- bzw. Ausgangsvariablen entsprechend der Identifizierung von Eingangs- und Ausgangsströmen der Units der chemischen Anlage. Sind für jedes nichtlineare Blocksystem neben den inneren Variablen auch die Ausgangsvariablen durch die Gleichungen des Blocks bestimmbar, so kann die Dimension des Koppelgleichungssystems im Vergleich zu den bisher verwendeten Verfahren vom Typ 1 auf etwa die Hälfte reduziert werden. Die Verfahren vom Typ 2 lassen sich besser parallelisieren als die Verfahren vom Typ 1. Da sich bei ihnen die Block-Sensitivitätsmatrizen der Ausgangsvariablen nach den Eingangsvariablen einfach berechnen lassen, sind sie außerdem gut für die Anwendung von Relaxationstechniken geeignet.

In Tabelle 1 ist ein Vergleich von Rechenzeiten für die Simulation mit BOP zum kommerziellen Prozeßsimulator SPEEDUP gegeben. Das Beispiel ist ein Reaktormodell, das auf einem Mehrphasen-Zellenmodell für die Reaktivseparation basiert. Im Vergleich zur Simulation mit SPEEDUP läßt sich die Rechenzeit mit BOP bei Verwendung von sechs Prozessoren um den Faktor 5.4 reduzieren. Dabei zeigt sich, daß die Typ 2-Verfahren im Vergleich zu den Typ 1-Verfahren eine effizientere Parallelisierung ermöglichen.

**Tabelle 1:** Dynamische Simulation von *Reaktor600* (n = 45 600 Gleichungen) auf Cray J90
Simulator	Anzahl	Anzahl	CPU time	Wall clock time
	Prozessoren	Blöcke	(sec.)	(sec.)
SPEEDUP	1	1	7 008	7 516
BOP	1	1	5 089	5 120
BOP mit BSN-Typ 1	1	18	5 814	5 870
BOP mit BSN-Typ 2	1	18	4 932	4 967
BOP mit BSN-Typ 1	6	18	6 208	1 904
BOP mit BSN-Typ 2	6	18	5 140	1 371

Die Diskretisierung der DAE-Systeme führt auf lineare Systeme mit schwachbesetzten Matrizen, die mit direkten Methoden behandelt werden. Während bei den wiederholten Faktorisierungen mit effektiven Pseudo-Code-Techniken gearbeitet wird, konnte nun auch die erste Faktorisierung durch eine besondere Bestimmung der Pivotspalte effektiver gestaltet werden. Einzelheiten sind im Projekttitel ,,Lineare Gleichungssysteme`` dargestellt, siehe S.

Aufbauend auf der Definition der Eingabesprache zur Beschreibung verfahrenstechnischer Prozesse wurde die Implementierung eines Compilers zur Erzeugung einer Schnittstelle zum Prozeßsimulator BOP weitergeführt. Die Erzeugung einer Listenstruktur aus der Analyse des Textes der Eingabesprache wurde implementiert und getestet. Hierbei wird die in der Modellierung verwendete Hierarchie berücksichtigt. Implementiert wurde ebenfalls die Auflösung dieser zweistufigen hierarchischen Struktur zu Listen, die den gesamten verfahrenstechnischen Prozeß beschreiben.

In Zusammenarbeit mit dem Max-Planck-Institut für Dynamik komplexer technischer Systeme (MPI) in Magdeburg wurde die automatische Erzeugung einer Schnittstelle aus Daten des Simulators SPEEDUP [5] erweitert. Es kann jetzt auch eine Schnittstelle zum an der Universität Stuttgart entwickelten Simulator DIVA erzeugt werden. Damit können Beispiele, die für den kommerziellen Simulator SPEEDUP entwickelt wurden, auch mit dem Simulator DIVA bearbeitet werden. Ebenso ist es möglich, für DIVA entwickelte Beispiele mit dem Simulator BOP zu rechnen. Die letztgenannte Arbeit wurde am MPI in Magdeburg durchgeführt und von uns unterstützt.

Weitere Arbeiten betreffen die Entwicklung von numerischen Verfahren für die von der Bayer AG, Leverkusen, entwickelte Simulationsumgebung Simulation Manager . Sie dient dem dynamischen Abgleich der Eingangs- und Ausgangskoppelströme von Teilprozessen eines verfahrenstechnischen Fließschemas für den Fall, daß die Teilprozesse in einem kleinen Zeitintervall unabhängig voneinander und verteilt in einem Rechnernetzwerk simuliert werden. Jeder Teilprozeß kann dabei separat modelliert und numerisch gelöst werden, wobei die in der chemischen Verfahrenstechnik eingesetzten kommerziellen Modellierungstools (z. B. SPEEDUP, gPROMS) verwendet werden können. Da diese Simulatoren im allgemeinen keine Eingangs- und Ausgangssensitivitäten liefern, werden ableitungsfreie Waveform-Iterationen untersucht. Die nachfolgende Darstellung geht vereinfachend davon aus, daß die p Teilprozesse durch DAE-Systeme

$\begin{eqnarray} F_j(t,y_j(t),\dot{y}_j(t),u_j(t)) = 0, & & j=1,...,p ,\nonumber \ [1mm] y_j(t)=(v_j(t),x_j(t))^T, && y_j(t_0)=y_j^0 \nonumber\end{eqnarray}$

beschrieben werden, wobei u_j(t) den Vektor der Eingangsvariablen des Teilprozesses j bezeichnet, während der Vektor v_j(t) die Ausgangsvariablen enthält.

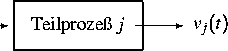
$\begin{picture} (100,40) \thicklines \put(0,0){ \framebox (80,30){Teilpro... ...){\vector(1,0){30}} \put(-56,13){$u_j(t)$} \put(116,13){$v_j(t)$}\end{picture}$

Die Vektoren x_j(t) enthalten die internen Prozeßvariablen. Es wird vorausgesetzt, daß die eingesetzten numerischen Verfahren die Ausgangsvektoren v_j(t)=G_j(u_j(t)) für gegebene Eingangsfunktionen u_j(t) mit ausreichender Genauigkeit berechnen. Das Fließschema des Gesamtprozesses ist dadurch gekennzeichnet, daß jede Komponente des Vektors aller Ausgangsvariablen v(t)=(v₁,...,v_p)^T genau einer Eingangsvariablen des Vektors u(t)=(u₁,...,u_p)^T zugeordnet ist. Es ist

$\begin{eqnarray} f\left(u(t)\right) \equiv u(t) - PG\left(u(t)\right)=0, \quad t \in [t_0,t_E], \nonumber\end{eqnarray}$

wobei die Permutationsmatrix P diese Zuordnung definiert. G repräsentiert die Gesamtheit aller nur implizit gegebenen Eingangs- und Ausgangsabbildungen G_j, j=1,...,p, der p Teilmodelle des Gesamtmodells.

Unter Berücksichtigung der durch den Simulation Manager vorgegebenen Beschränkungen wird auf einem äquidistant unterteilten Teilintervall des Simulationsbereiches [t₀,t_E] eine diskrete Lösung mit

$\begin{eqnarray} v_j^{k+1} &=& G_j(u_j^k), \quad j=1,...,p, \nonumber \ [1mm] u^{k+1} &=& Pv^{k+1}, \quad k=0,1,... \nonumber\end{eqnarray}$

iterativ bestimmt (Waveform-Iterationsverfahren). Arbeiten zur Konvergenzbeschleunigung auf der Grundlage von quasi-Newton-Verfahren, insbesondere bei stark verkoppelten Systemen, wurden durchgeführt. Dazu erfolgte die Entwicklung verschiedener anwendungsnaher Testbeispiele und ihre Erprobung mit dem Simulation Manager (siehe Abb. 1).