[Next]:

Intermittierende Dynamik

[Up]:

Projektbeschreibungen

[Previous]:

Projektbeschreibungen

 [Contents] 

 [Index] 

Nichtlineare Dynamik von DFB-Halbleiterlasern

Bearbeiter: M. Radziunas , K. R. Schneider , J. Sieber , M. Wolfrum  

Kooperation: U. Bandelow (FG 1), L. Recke (Institut für Mathematik, HU Berlin), B. Sartorius, D. Hoffmann (Heinrich-Hertz-Institut für Nachrichtentechnik Berlin), H.-J. Wünsche (Institut für Physik, HU Berlin), H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin)

Beschreibung der Forschungsarbeit:

Mehrsektions-DFB-Halbleiterlaser besitzen nichtlineare Phänomene, wie z. B. hochfrequente Selbstpulsationen und Schalteffekte, die sie zu wichtigen Bauelementen in zukünftigen Nachrichtennetzen mit rein optischer Signalverarbeitung prädestinieren. Gegenstand dieses längerfristigen Projektes sind Fragen der mathematischen Modellierung des komplexen Verhaltens derartiger Laser sowie analytische und numerische Untersuchungen der entsprechenden Differentialgleichungssysteme.

Zur mathematischen Modellierung der Dynamik von Halbleiterlasern verwenden wir ein dissipatives hyperbolisches System partieller Differentialgleichungen (travelling-wave-Gleichungen), das mit einem System gewöhnlicher Differentialgleichungen (Ladungsträger-Gleichungen) gekoppelt ist:

    $$\begin{eqnarray} \frac{\partial \psi}{\partial t} & = & iH (n,z) \psi , \ \fra... ..._k^2) \mbox{\hspace*{3em} für $k=1$, \ldots Anzahl der Sektionen.}\end{eqnarray}$$

Zusätzlich werden noch Randbedingungen für die Reflexion an den Laserfacetten verwendet. $\psi$ ist der Vektor der Feldamplituden für die vorwärts- und rückwärtslaufende Welle, n beschreibt die Ladungsträgerdichte. Im Berichtszeitraum wurden Forschungen zu folgenden Fragestellungen durchgeführt:

1.

Weiterentwicklung der Software TLP,

2.

Numerische Untersuchungen der Dynamik von Halbleiterlasern,

3.

Modellerweiterung.

1. Software. Die Software TLP wurde wie folgt weiterentwickelt.

a.

Zur Lösung der Differentialgleichungen wurde ein endliches Differenzverfahren vom Prädiktor-Korrektor-Typ implementiert.

b.

Es wurde ein reduziertes Modell (Vernachlässigung von Lochbrenneffekten) implementiert, das eine drastische Rechenzeitverkürzung gestattet.

c.

Um den Einfluß der Polarisation auf die Laserdynamik studieren zu können, wurde ein erweitertes Modell (siehe unten) implementiert.

d.

Das Programmsystem wurde so modifiziert, daß die Einwirkung externer Signale auf das Laserverhalten (und somit das wichtige Synchronisationsverhalten) numerisch untersucht werden kann.

e.

Es wurden Möglichkeiten zur graphischen Darstellung und zur Ausgabe der erhaltenen Datenfiles geschaffen.

2. Numerische Untersuchungen. Die numerischen Untersuchungen dienen zur Optimierung der Laserdynamik (Bauelementeoptimierung). Das Differentialgleichungssystem (1), (2) zur Beschreibung der Laserdynamik hängt von zahlreichen Parametern ab. Der Operator H kann durch den folgenden Matrix-Operator dargestellt werden:

$$iH = v_g \left( \begin{array} {cc} i \frac{\partial}{\partia... ... i \frac{\partial}{\partial z} - \beta (z,t)\end{array}\right).$$

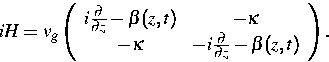
Dabei ist $\beta (z,t)$ die komplexwertige Ausbreitungsfunktion des Wellenleiters, die unter Verwendung der Modellfunktion

$$\beta (z,t) = \beta_0 - i \frac{\alpha_0}{2} + (\alpha_H + i) \frac{g}{2}\cdot (n(t) - n_{tr})$$

dargestellt wird.

Für den zu berechnenden 3-Sektions-DFB-Halbleiterlaser wird angenommen, daß zwei Lasersektionen durch eine passive Phasensektion separiert sind, wobei an einer DFB-Sektion ein großer Pumpstrom angelegt wird (Gain-Sektion), während die andere einen vergleichsweise niedrigen, aber festgelegten Pumpstrom aufweist (Reflektorsektion). Das Ziel der numerischen Untersuchungen besteht darin, Gebiete im Parameterraum zu bestimmen, so daß den Punkten dieser Teilgebiete Systeme (1), (2) mit speziellen Eigenschaften entsprechen. Zu den zu optimierenden Eigenschaften gehören u. a. die Robustheit bestimmter Qualitäten gegenüber Störungen und die Existenz von Selbstpulsationen mit hohen Frequenzen. Es wurden numerische Untersuchungen hinsichtlich folgender Fragestellungen durchgeführt:

a. Robustheit von Selbstpulsationen  

Das Ziel bestand in der Untersuchung des Einflusses der Lasergeometrie auf die Existenz von möglichst großen zusammenhängenden Parametergebieten, denen Systeme (1), (2) mit Selbstpulsationen hoher Frequenz entsprechen. Die folgenden Abbildungen zeigen den Einfluß der Länge der Phasensektion auf die Existenz derartiger Parametergebiete.

 

Abb. 1:

b. Hysterese   bei Parameterstörungen

Die Untersuchungen zur Persistenz der Selbstpulsationen gegenüber Parameteränderungen weisen eine deutliche Abhängigkeit gegenüber der Richtung der Parameteränderung auf. Die folgenden Abbildungen zeigen die Existenz von Selbstpulsationen im Parametergebiet $\mbox{Re } \beta_g /\mbox{Re } \beta_p$.

 

Abb. 2:  

Die Bedeutung des horizontal und vertikal schraffierten Gebietes von Abb. 2 besteht darin, daß die zugehörigen Selbstpulsationen auch bei Änderungen über den Rand des dargestellten Gebietes hinaus persistieren. Die Existenz von Hysterese ist an die Existenz von Bistabilität gebunden, sie impliziert die Existenz von Sattel-Knoten-Bifurkationen für periodische Lösungen.

c. Frequenzoptimierung  

Die numerischen Untersuchungen zeigen eine Zunahme der Frequenz der Selbstpulsationen, falls der Pumpstrom der Gain-Sektion erhöht wird. Derselbe Effekt kann bei einer Rotverschiebung des optischen Feldes beobachtet werden (Abb. 3). Die numerischen Untersuchungen wurden im Experiment bestätigt.

 

Abb. 3:  

3. Modellerweiterung.   Für eine realistische Beschreibung des Lasers im mehrmodigen Betrieb muß die Dispersion des optischen Gewinns in einem entsprechend breiten Frequenzbereich berücksichtigt werden. Das System (1) enthält nur eine lineare Indexdispersion und frequenzunabhängige Gewinne. Um nichtlineare Dispersion beschreiben zu können, werden an (1) zusätzliche Polarisationsgleichungen gekoppelt [1]:

    $$\begin{eqnarray} \frac{\partial \psi}{\partial t} & = & iH\left(\psi - \frac{g_r... ...rtial p}{\partial t} & = & i(\Gamma \psi + (\delta + i \Gamma )p).\end{eqnarray}$$

Der maximale Gewinn $g_r (z) \ge 0,$ die Halbwertsbreite $\Gamma (z) \gt 0$ und die relative Resonanzfrequenz $\delta (z)$ werden aus Meßergebnissen von realen Lasern gewonnen und als stückweise konstant angenommen. Die Ankopplung der Polarisation in (3), (4) entspricht einer Approximation der Gewinnkurve in der Nähe der zentralen Frequenz $\omega_0$ durch eine Lorentzkurve

$${\cal{X}} (\omega) = \frac{g_r (z) \Gamma (z)}{2 (\omega - \omega_0 - \delta (r) - i\Gamma (z)}\ .$$

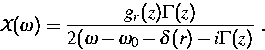
Projektliteratur:

1.  J. SIEBER, U. BANDELOW, H. WENZEL, M. WOLFRUM, H.-J. WÜNSCHE, Travelling wave equations for semiconductor lasers with gain dispersion , WIAS-Preprint, No. 459 , 1998.

[Next]:

Intermittierende Dynamik

[Up]:

Projektbeschreibungen

[Previous]:

Projektbeschreibungen

 [Contents] 

 [Index]