Hysteresephänomene in Magnetoelastizität und Thermoelastoplastizität

Bearbeiter: M. Siegfanz, J. Sprekels 

Kooperation: M. Brokate, Christian-Albrechts-Universität zu Kiel,
P. Krejcí, Tschechische Akademie der Wissenschaften, Prag

Beschreibung der Forschungsarbeit:

Ziel dieses Projektes ist es, realistische Modelle für die Evolution von Systemen herzuleiten, in denen Nichtlinearitäten vom Hysterese-Typ auftreten. Von besonderem Interesse für die Anwendungen sind dabei Fragen der elastischen Verformung von Ferromagneten in magnetischen Feldern (Magnetostriktion) und der Temperaturabhängigkeit elastoplastischer Hysteresen in Stählen oder Legierungen mit Formgedächtnis.

Zum erstgenannten Thema wurde ein eindimensionales Modell entwickelt, das in vereinfachter Form auf die Feldgleichungen

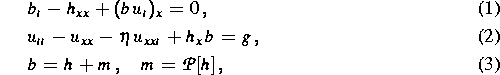
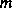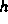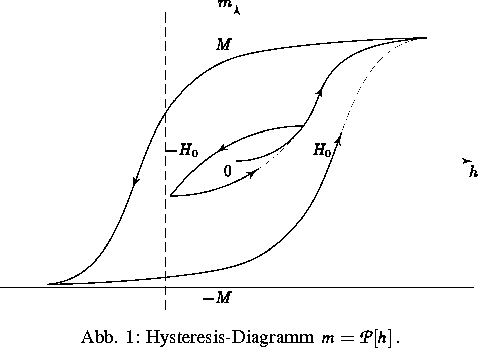
mit geeigneten Anfangs- und Randbedingungen führt; dabei wird die ferromagnetische Hysterese zwischen der Magnetisierung und dem magnetischen Feld in Form einer Operatorgleichung 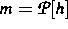mit einem Hysteresis-Operator vom Preisach-Typ (vgl. [1]) modelliert.

Es gelang, globale Existenz von (schwachen) Lösungen sowohl für den viskosen (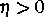) als auch für den nichtviskosen (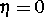) Fall nachzuweisen (im letzteren Fall allerdings nur für kleine Daten). In Zukunft sollen mehrdimensionale Situationen untersucht werden, die für den Effekt der Magnetostriktion relevant sind.

Mathematische Modelle der Elastoplastizität im isothermen Fall beruhen meistens entweder auf der Verwendung von Variationsungleichungen oder der wesentlich allgemeineren Hysteresis-Operatoren vom PRANDTL-ISHLINSKII-Typ (vgl. [1]). Die Einbeziehung der Temperatur als zusätzlicher Zustandsvariable bereitet im Fall der Hysteresis-Operatoren grundsätzliche Schwierigkeiten, da nicht klar ist, wie dann die thermodynamischen Potentiale freie Energie, innere Energie und Entropie definiert und der Erste und Zweite Hauptsatz der Thermodynamik angewendet werden können.

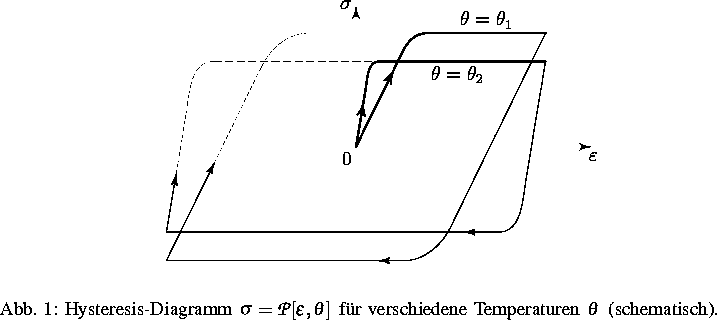
In [2] ist es nunmehr erstmalig gelungen, für temperaturabhängige PRANDTL-ISHLINSKII-Operatoren der Form

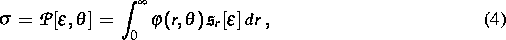
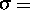( Spannung, 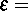Verzerrung, 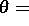absolute Temperatur, 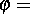Dichtefunktion, 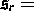elastisch-plastisches Element zur Schwelle 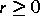) eine thermodynamisch konsistente Theorie der Thermoplastoelastizität zu entwickeln. Die grundlegende Idee beruht darauf, die in [1] ausgeführte Theorie der Hysteresis-Potentiale zu verallgemeinern. Freie Energie, innere Energie und Entropie ergeben sich dann als Operatoren, nicht länger als Funktionen, und man erhält eine Thermodynamik von Operatoren. Weiterentwicklungen dieses Konzeptes wurden in den Arbeiten [3,4] vorgenommen.

Für den einfachsten eindimensionalen Fall erhält man Zustandsgleichungen der Form (Massendichte 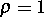gesetzt)

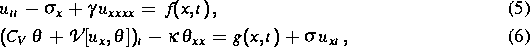
wobei 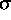durch (4) und 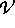durch

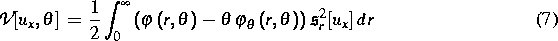
gegeben sind. In [2] wurde die Existenz einer (schwachen) Lösung 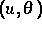für eine Anfangs-Randwertaufgabe für dieses System gezeigt, in [3, 4] wurden diese Resultate verallgemeinert.

Aufgrund der erzielten Ergebnisse steht nun erstmalig ein sehr allgemeiner thermodynamisch konsistenter Ansatz zur mathematischen Modellierung von Problemen der Thermoelastoplastizität zur Verfügung. Die Arbeit an dieser Problemstellung soll im kommenden Jahr intensiviert werden.

Projektliteratur:

1. M. BROKATE, J. SPREKELS, Hysteresis and Phase Transitions, Applied Mathematical Sciences Vol. 121, Springer-Verlag, New York 1996.
2. P. KREJCÍ, J. SPREKELS, On a system of nonlinear PDE's with temperature-dependent hysteresis in one-dimensional thermoplasticity, WIAS-Preprint No. 219, Berlin 1996; erscheint in: J. Math. Anal. Appl.
3. P. KREJCÍ, J. SPREKELS, Towards a thermodynamic theory of hysteresis operators: One-dimensional thermoplasticity, in Vorbereitung.
4. P. KREJCÍ, J. SPREKELS, One-dimensional thermovisco-elastoplasticity with hysteresis, in Vorbereitung.
5. P. KREJCÍ, J. SPREKELS, Global solutions to a coupled parabolic-hyperbolic system with hysteresis in 1-d magnetoelasticity, WIAS-Preprint No. 237, Berlin 1996; erscheint in: Nonlin. Anal. TMA.