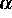Spin-Gläser und Neurale Netze

Bearbeiter: A. Bovier

Förderung: EU, CHRX-CT93-0411

Kooperation: V. Gayrard (CPT-Marseille), P. Picco (CPT-Marseille)

Beschreibung der Forschungsarbeit:

Eine ausführliche Darstellung der Fragestellungen, denen wir uns in diesem Projekt widmen, wurde im Jahresbericht 1994 gegeben. Im diesem Jahr wurden eine Reihe von wichtigen neuen Resultaten erzielt. So wurde in der Arbeit [1] unter schwächstmöglichen Voraussetzungen ein Prinzip großer Abweichungen für die Verteilung der (unendlich vielen) Ordnungsparameter im Hopfield Modell bewiesen. Dies bedeutet, daß ein perfektes thermodynamisches Verhalten mit deterministischen thermodynamischen Potentialen für dieses ungeordnete Modell mit unendlich vielen relevanten Ordnungsparametern vorliegt. In der Praxis noch relevantere Resultate wurden in [2] für den Fall, daß die Zahl der ,,pattern`` proportional zur Systemgröße skaliert, gezeigt. Hier wurden alle wesentlichen heuristischen Erwartungen bezüglich des Verhaltens des Modells für kleine Proportionalitätsfaktoren 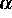mathematisch rigoros bewiesen. Dabei wurden Methoden zur Analyse komplizierter Zufallsfunktionen unbeschränkt vieler Variablen entwickelt, die auch in anderen Fragen der statistischen Mechanik ungeordneter Systeme von Nutzen sein werden.

Die schon im Vorjahr begonnene Untersuchung von Varianten des Hopfield Modells mit lang, aber endlich reichweitiger Wechselwirkung (,,Kac-Hopfield Modell``) [3], wurde ebenfalls intensiv weiter betrieben. Insbesondere geht es uns nunmehr darum, diese Modelle auf mesoskopischer Ebene zu charakterisieren. Das heißt, wir betrachten lokale Ordnungsparameter und untersuchen deren Verteilung unter dem Gibbs Maß bei geeigneter Skalierung. Dabei ergibt sich asymptotisch eine Beschreibung durch eine Ginzburg-Landau-artige Feldtheorie, wobei das entsprechende Funktional aber noch zufällig ist. Technisch ist die Kontrolle der Approximationsfehler hier äußerst aufwendig. Die Untersuchung des eindimensionalen Falles steht zur Zeit vor dem Abschluß [4]. Im höherdimensionalen Fall sind noch erhebliche Schwierigkeiten zu überwinden, was wohl noch geraume Zeit in Anspruch nehmen wird.

Projektliteratur:

1. A. BOVIER, V. GAYRARD, An almost sure large deviation principle for the Hopfield model, WIAS-Preprint No. 146 (1995), erscheint in Ann. Probab., (1996).
2. A. BOVIER, V. GAYRARD, The retrieval phase of the Hopfield model: A rigorous analysis of the overlap distribution, WIAS-Preprint No. 161 (1995), eingereicht bei Prob. Theor. Rel. Fields (1995).
3. A. BOVIER, V. GAYRARD, P. PICCO, Large deviation principles for the Hopfield model and the Kac-Hopfield model, Prob. Theor. Rel. Fields 101, 511-546 (1995).
4. A. BOVIER, V. GAYRARD, P. PICCO, Distribution of overlap profiles in the one-dimensional Kac-Hopfield model, in Vorbereitung.