



Bearbeiter: R. J. Rumpel
Beschreibung der Forschungsarbeit:
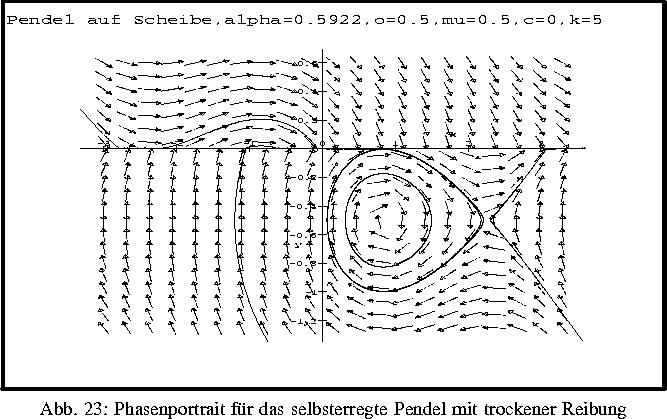
Systeme gewöhnlicher Differentialgleichungen mit Unstetigkeitsflächen stellen bei vielen Anwendungen ein geeignetes Modell dar. Zum Beispiel tritt bei Schwingungen mit trockener Reibung oder bei Systemen mit Relaissteuerung die unstetige Signumfunktion in der beschreibenden Gleichung auf. Bei solchen Systemen kann es zu Bewegungen auf der Unstetigkeitsfläche kommen. In diesem Fall ist es nicht ausreichend, das System als Differentialinklusion zu interpretieren. Als eine Möglichkeit zur Beschreibung der Dynamik auf der Unstetigkeitsfläche dient die Methode der äquivalenten Steuerung.

Das Ziel der Untersuchungen besteht darin, qualitative Aussagen über das Verhalten solcher Systeme herzuleiten. Bei selbsterregten nichtlinearen Schwingungen mit trockener Reibung mit einem Freiheitsgrad konnte gezeigt werden, unter welchen Bedingungen ein homokliner Orbit persistiert und wann Grenzzykeln existieren. Von Interesse ist darüber hinaus das Verhalten höherdimensionaler Systeme. Hierbei wird die Theorie singulär gestörter Systeme auf Differentialgleichungen mit Unstetigkeiten angewandt. Ergebnisse zur asymptotischen Darstellung entsprechender Lösungen liegen vor.
Projektliteratur: