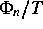 ,
, 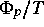 und
und 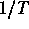 beschrieben werden sollten, wenn
beschrieben werden sollten, wenn
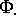 die elektrochemischen Potentiale der Elektronen und der
Löcher bezeichnet und T die Temperatur ist,
die elektrochemischen Potentiale der Elektronen und der
Löcher bezeichnet und T die Temperatur ist,
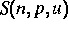 der Entropie und auf dessen
konjugiertem Potential
der Entropie und auf dessen
konjugiertem Potential 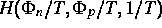 beruht.
beruht.




Bearbeiter: G. Albinus
Kooperation: G. Wachutka, Lehrstuhl für technische Elektrophysik, TU München;
K. Gärtner, Institut für Integrierte Systeme, Eidgenössische Technische Hochschule Zürich;
B. Heinemann, Institut für Halbleiterphysik, Frankfurt/Oder;
U. Todt, Fraunhofer-Institut für Mikroelektronische Schaltungen und Systeme, Dresden
Beschreibung der Forschungsarbeit:
Ziel des Projektes ist die selbstkonsistente Temperaturberechnung in Halbleiterbauelementen auf der Grundlage phänomenologischer Energiemodelle. Solche Modelle werden durch ein System von vier partiellen Differentialgleichungen beschrieben. Das System besteht aus der Poissongleichung für das elektrostatische Potential und aus drei Transportgleichungen für den Elektronen- und Löchertransport sowie für die Wärmeleitung. Auf Grund der Zustands- und Stromgleichungen ist das System ausgeprägt nichtlinear. Erfahrungen mit dem Drift-Diffusionsmodell und auch mit dem Energiemodell zeigen, daß die Berücksichtigung der thermodynamischen Struktur der Prozesse von großer praktischer Bedeutung für die numerische Simulation ist. Unter diesem Gesichtspunkt ist der Übergang vom Drift-Diffusionsmodell zum Energiemodell eine wesentliche Veränderung, die sich keineswegs in dem quantitativen Aspekt einer zusätzlichen parabolischen Gleichung erschöpft.
In dem Berichtszeitraum wurde diese Struktur untersucht und beschrieben. Es zeigt sich dabei, daß
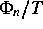 ,
, 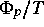 und
und 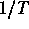 beschrieben werden sollten, wenn
beschrieben werden sollten, wenn
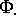 die elektrochemischen Potentiale der Elektronen und der
Löcher bezeichnet und T die Temperatur ist,
die elektrochemischen Potentiale der Elektronen und der
Löcher bezeichnet und T die Temperatur ist,
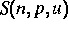 der Entropie und auf dessen
konjugiertem Potential
der Entropie und auf dessen
konjugiertem Potential 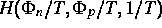 beruht.
beruht.
Diese Ergebnisse sind in der bisherigen Simulationspraxis nicht berücksichtigt und werfen auch Fragen auf, die in Zusammenarbeit mit Fachleuten der irreversiblen Thermodynamik zu besprechen sind. Außerdem sollten die Ergebnisse über den Rahmen der Halbleitergleichungen hinaus überall dort von Interesse sein, wo eine nicht-lokale Wechselwirkung wie die elektrostatische auftritt und die Temperatur oder eine äquivalente Zustandsgröße eine dynamische Variable ist.
Projektliteratur:



