Bearbeiter: H. Schurz
Kooperation: Karmeshu (Jawaharlal Nehru University, New Delhi), F. Delbaen (ETH, Zürich), U. Küchler (Humboldt-Universität, Berlin)
Förderung: SFB 373 ,, Quantifikation und Simulation ökonomischer Prozesse``
Beschreibung der Forschungsarbeit:
Bei der Modellierung und Simulation von Finanzinstrumenten (Derivate, Optionen) spielt mehr und mehr das dynamische Verhalten von stochastischen Zinsraten und Zinsstrukturkurven eine entscheidende Rolle. Die Entwicklung und Erforschung von Zinsraten- und Preismodellen erfordert adäquate analytische und numerische Techniken und Simulationsstudien dieser Prozesse. Wir verbinden den Erkenntnisstand über die moderne Theorie zum qualitativen Verhalten stochastischer dynamischer Systeme mit der Leistungsfähigkeit stochastisch-numerischer Verfahren. Als Modellklasse untersuchen wir die in [4] vorgeschlagenen verallgemeinerten stochastischen Differentialgleichungen
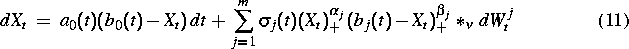
zur Modellierung nichtnegativer Zinsraten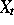 
mit
deterministischen nichtnegativen Parametern 
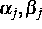und fixem
stochastischen
Kalkülparameter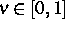 
(0 entspricht dem
Itô-Kalkül).
Fast alle zeitstetigen Markovschen Zinsratenmodelle sind darin
enthalten, z. B.
die Modelle von Vasicek, Cox-Ingersoll-Ross, Dothan,
Courtadon und Chan. Erste Resultate hinsichtlich strenger
Existenz, Eindeutigkeit und fast
sicherer Beschränktheit der Lösung konnten
erzielt werden, siehe [4]. Dazu benutzten wir die Technik stochastischer
Lyapunov-Funktionen und die
Dynkins Formel. Adäquate numerische Lösungen dafür sind
derzeit nur durch
geeignete implizite Balance-Methoden (BIMs) konstruierbar. Es
gelang,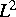 
-Konvergenz und fast sichere numerische Beschränktheit ohne
Zuhilfenahme von
Projektionsmethoden zu verifizieren. Umfangreiche
Simulationsstudien, die in
[2], [3] und [5] für den Besselprozeß begonnen wurden, bestätigen
diese Aussage.
Das obige Modell zeigt eine große Vielfalt von qualitativen
Eigenschaften (z. B. Markov pseudo switching), die eine enorme
Anpassungsfähigkeit an reale
Datensätze garantieren. Zum Beispiel gibt es
eine einfache Teilklasse, die Nichtnegativität, zweiseitige
Beschränktheit und
zwei zeitweilig anziehende Levels besitzt.
Ein qualitativ ähnliches Verhalten tritt im stochastischen
Marketing auf.
Das BASS Modell beschreibt, wie sich ein Produkt, eine neue
Technologie, Idee,
Neuigkeiten, Gerüchte im zu beobachtenden Medium (Markt)
ausbreiten.
Erstmals wurde in [1] ein entsprechendes stochastisches Modell
zur Modellierung
der Diffusion von Innovationen vorgestellt und simuliert. Es ist
eine Verallgemeinerung des deterministischen BASS Modells unter
Berücksichtigung von
Parameterschwankungen und einer gewissen Ungewißheit im Markt/Medium.
So wird angenommen, daß sich die Anzahl der Adoptionen 
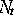durch die Itô
Differentialgleichung
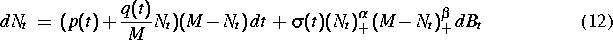
mit p>0 als Koeffizient der Innovation, q>0 als Koeffizient der Imitation und M>>1 als maximale Anzahl möglicher Adoptionen beschreiben läßt. In Analogie zu den obigen Problemen im Finanzwesen werden die analytische und numerische Lösung untersucht. Die mathematische Rechtfertigung findet sich in [6], Simulationsergebnisse dazu in [1] und [6]. Hauptergebnis ist die Erkenntnis, daß Ungewißheit in parametrischer oder in modellierender Form zu erheblichen Unterschieden im qualitativen Verhalten gegenüber dem deterministischen Modell führt. Zum Beispiel kann der ,,point of inflection'', der Punkt der höchsten Marktnachfrage, unter zufälligen Einflüssen deutlich früher erreicht werden. Dies dürfte eine wesentliche Information für die Praxis des Marketing sein. Aufgrund der Nichtlinearität des Modells sind weitere interessante Studien (wie Niveauüberschreitungen oder Persistenz) zu erwarten.
Projektliteratur: