



Bearbeiter: H. Schurz
Kooperation: Karmeshu (Jawaharlal Nehru University, New Delhi), G. I. Schueller (TU, Innsbruck), L. Möller (ETH, Zürich), H. C. Öttinger (ETH, Zürich), C. Bucher (FH, Weimar), G. Denk (TU, München), F. M. Reich (BMW, München)
Beschreibung der Forschungsarbeit:
Im Mittelpunkt dieses Projekts stehen Fragen der Anwendung stochastischer Modellierung, Analysis und Simulation in ausgewählten Gebieten aus Technik- und Ingenieurwissenschaften, wie z. B. Hydrologie, Seismologie, Kommunikationstechnik und in der Polymerenphysik.

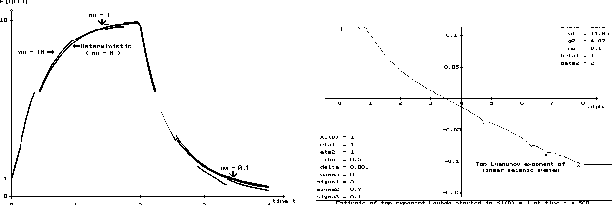
Abb. 1 - 2: Mittlere Abflußrate | Größter Lyapunov Exponent
Erste konkrete Ergebnisse liegen in der Hydrologie und Seismologie bereits vor, wie z. B. Untersuchungen zur stochastischen Modellierung und Schätzung der zeitlichen Momentenentwicklungen von nichtlinearen Abflußraten in Wasserreservoirs [3]. Eine Schätzung des ersten Moments des Abflusses von einem nichtlinearen Reservoir bei exponentiell abklingender Regenfallintensität ist im ersten Bild zu sehen. Stationäre Lösungen der auftretenden Fokker-Planck-Kolmogorov-Gleichung der nichtlinearen Abflußrate konnten exakt berechnet werden. In der Seismologie (siehe [1],[2]) gelang es uns, nichtkonstante Delayterme in höherdimensionalen stochastischen Integrodifferentialsystemen sowohl theoretisch als auch numerisch zu behandeln. Die auftretenden seismischen Störungen und Rauschquellen führen zu einer signifikanten Amplifikation und zu einer Phasenverschiebung der stochastischen Oszillationen (Destabilisierung). Des weiteren untersuchten wir die Stabilität der zugehörigen Momentenentwicklungen. Notwendige und hinreichende Bedingungen für die Stabilität der ersten beiden Momente der linearisierten Dynamik sind in [1] angegeben. Durch die Natur seismischer Störungen ist es naheliegend, auch das pfadweise Stabilitätsverhalten der zu modellierenden Baukonstruktion zu erforschen. Die mathematische Grundlage dazu bildet die Theorie und Schätzung von Lyapunov-Exponenten. Untersucht wurden u. a. die Abhängigkeit dieser Exponenten von der Kontrollgeschwindigkeit, die im mechanischen System zum Aufbau der Kontrollkräfte für dessen Stabilisierung notwendig ist, vgl. Abb. 2. Außerdem wurden Wahrscheinlichkeiten der kritischen Niveauüberschreitung numerisch geschätzt (Abb. 3) sowie Phasendiagramme des nichtlinearen Systems visualisiert (Abb. 4).
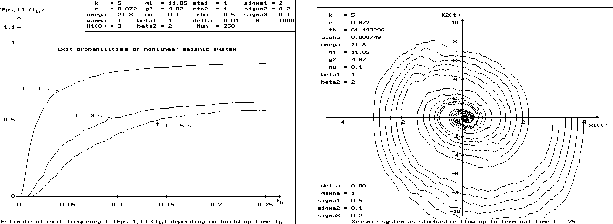
Abb. 3 - 4: Kritische Austritts-Wahrscheinlichkeiten | Phasenporträt eines kubischen Oszillators
Im Rahmen dieses Projektes fand eine Sichtung weiterer potentieller Anwendungsmöglichkeiten der stochastischen Analysis und Numerik statt.
Projektliteratur:



