



Next: Stabilität und Konvergenz
Up:
Previous: Optimale nichtparametrische Verfahren
Bearbeiter: M. Nussbaum
Kooperation: I. Grama (Kishinev, Moldawien), A. Gushchin
(Moskau), P. Hall (Canberra), A. Korostelev (Detroit), M. Low
(Philadelphia), S. van de Geer (Leiden)
Förderung: DAAD, DFG, HCM-Netzwerk ,,Statistics of Stochastic
Processes''
Beschreibung der Forschungsarbeit:
Die grundlegende Aufgabe in diesem Gebiet ist die Approximation
allgemeiner statistischer Modelle durch einfachere; es entsteht
dabei eine Theorie, die sich abstrakter Konzepte bedient und die
(in der Tragweite für die Statistik) etwa der Funktionalanalysis
vergleichbar ist. Der Schwerpunkt der Untersuchungen liegt bei
den nichtparametrischen, d. h. unendlichdimensionalen Problemen;
eingeschlossen sind stochastische inverse Probleme der Tomographie
und Bildverarbeitung, Zusammenhänge zur entsprechenden
deterministischen Theorie sowie die Statistik stochastischer
Differentialgleichungen.
Ein zentrales Thema in diesem Zusammenhang war die asymptotische
Äquivalenz nichtparametrischer Experimente zu Gaußschen
Folgen, im Sinne des Le Cam'schen Defizienzabstandes. Die
Arbeiten zur globalen Approximation für Modelle aus
unabhängigen, identisch verteilten Zufallsvariablen konnten
abgeschlossen werden (s. [7]), im grundlegenden Fall glatter,
nach unten beschränkter Dichten auf dem Einheitsintervall.
Daran anschließend wurden nichtgaußsche Regressionsmodelle
untersucht [2]; der Nachweis der asymptotischen Äquivalenz zu
Gaußschen Experimenten gelang durch Einsatz einer
entsprechenden funktionalen KMT-Ungleichung für den
Partialsummenprozeß nicht identisch verteilter Zufallsvariabler
[1]. In Analogie zu Gaußschen Approximationen sind auch
Poissonsche begleitende Folgen nichtparametrischer Experimente
von Interesse; hier konnte ein entsprechendes Resultat von Le Cam
für Produktexperimente wesentlich erweitert werden (für
Glattheitsgrade der Dichte unter 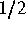 , s. [4]). Vorbereitende
Arbeiten für die Behandlung allgemeinerer Semimartingal-Modelle
wurden im parametrischen Rahmen der Verzweigungsprozesse
durchgeführt, vgl. [3].
Das Studium nichtparametrischer Experimente ist motiviert durch
Glättungsaufgaben bei stochastischen inversen und schlecht
gestellten Problemen. Die Untersuchungen über optimale
Konvergenzgeschwindigkeiten für Schätzungen von Konturen der
Trägergebiete von Wahrscheinlichkeitsdichten [5] stellten
gleichzeitig eine Verbindung zu den Fragen nach
Grenzexperimenten in der Extremwerttheorie her. Eine Anwendung
der asymptotischen Äquivalenztheorie auf das Problem der exakten
Risikoasymptotik bei der Dichteschätzung wurde in [6] gegeben.
, s. [4]). Vorbereitende
Arbeiten für die Behandlung allgemeinerer Semimartingal-Modelle
wurden im parametrischen Rahmen der Verzweigungsprozesse
durchgeführt, vgl. [3].
Das Studium nichtparametrischer Experimente ist motiviert durch
Glättungsaufgaben bei stochastischen inversen und schlecht
gestellten Problemen. Die Untersuchungen über optimale
Konvergenzgeschwindigkeiten für Schätzungen von Konturen der
Trägergebiete von Wahrscheinlichkeitsdichten [5] stellten
gleichzeitig eine Verbindung zu den Fragen nach
Grenzexperimenten in der Extremwerttheorie her. Eine Anwendung
der asymptotischen Äquivalenztheorie auf das Problem der exakten
Risikoasymptotik bei der Dichteschätzung wurde in [6] gegeben.
Projektliteratur:
- I. GRAMA, M. NUSSBAUM, A functional KMT approximation
for partial sums of independent variables, in Vorbereitung.
- I. GRAMA, M. NUSSBAUM, Asymptotic equivalence of
regression experiments, in Vorbereitung.
- A. GUSHCHIN, On efficiency bounds for estimating the
offspring mean in a branching process, WIAS-Preprint No. 175 ,
Berlin, 1995.
- M. LOW, M. NUSSBAUM, S. VAN DE GEER, Poissonization
of product experiments, in Vorbereitung.
- P. HALL, M. NUSSBAUM, S. STERN, On the estimation
of a support curve of indeterminate sharpness, Technical report,
Australian National University, Canberra, 1995.
- A. KOROSTELEV, M. NUSSBAUM, Density estimation in
the uniform norm and white noise approximation, WIAS-Preprint
No. 154, Berlin, 1995.
- M. NUSSBAUM, Asymptotic equivalence of density
estimation and Gaussian white noise, WIAS-Preprint No. 174,
Berlin, 1995, erscheint in: Ann. Statist., 1996.




Next: Stabilität und Konvergenz
Up:
Previous: Optimale nichtparametrische Verfahren
Group_of_Office
Mon May 13 20:25:53 MET DST 1996
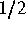 , s. [4]). Vorbereitende
Arbeiten für die Behandlung allgemeinerer Semimartingal-Modelle
wurden im parametrischen Rahmen der Verzweigungsprozesse
durchgeführt, vgl. [3].
Das Studium nichtparametrischer Experimente ist motiviert durch
Glättungsaufgaben bei stochastischen inversen und schlecht
gestellten Problemen. Die Untersuchungen über optimale
Konvergenzgeschwindigkeiten für Schätzungen von Konturen der
Trägergebiete von Wahrscheinlichkeitsdichten [5] stellten
gleichzeitig eine Verbindung zu den Fragen nach
Grenzexperimenten in der Extremwerttheorie her. Eine Anwendung
der asymptotischen Äquivalenztheorie auf das Problem der exakten
Risikoasymptotik bei der Dichteschätzung wurde in [6] gegeben.
, s. [4]). Vorbereitende
Arbeiten für die Behandlung allgemeinerer Semimartingal-Modelle
wurden im parametrischen Rahmen der Verzweigungsprozesse
durchgeführt, vgl. [3].
Das Studium nichtparametrischer Experimente ist motiviert durch
Glättungsaufgaben bei stochastischen inversen und schlecht
gestellten Problemen. Die Untersuchungen über optimale
Konvergenzgeschwindigkeiten für Schätzungen von Konturen der
Trägergebiete von Wahrscheinlichkeitsdichten [5] stellten
gleichzeitig eine Verbindung zu den Fragen nach
Grenzexperimenten in der Extremwerttheorie her. Eine Anwendung
der asymptotischen Äquivalenztheorie auf das Problem der exakten
Risikoasymptotik bei der Dichteschätzung wurde in [6] gegeben.



