



Bearbeiter: H.-J. Mucha, R. Siegmund-Schultze
Kooperation: K. Dübon, Forschungszentrum Daimler-Benz, Ulm
Beschreibung der Forschungsarbeit:
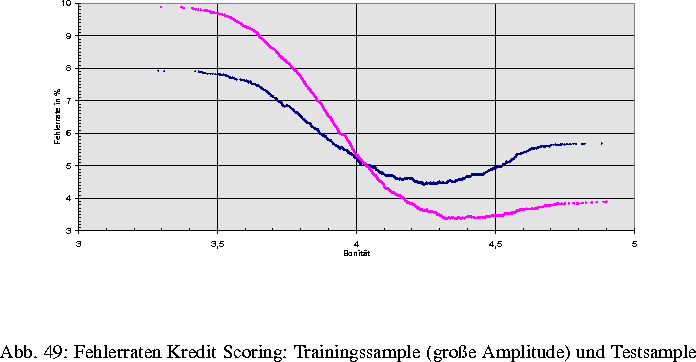
Kreditgeber (Banken, Kaufhäuser, etc.) sind bei der Vergabe von Krediten daran interessiert, daß sowohl die Rückzahlung der Kreditsumme als auch die Begleichung von Bearbeitungsgebühren und entstehenden Zinsen ordnungsgemäß abgewickelt wird. Für die Kredit(karten)geber ist es daher wichtig, die zukünftige Bonität eines potentiellen Kreditnehmers abzuschätzen. Die computerorientierte Statistik wird stark gefordert: Es sind sehr umfangreiche Datenmengen, bestehend aus numerischen und alphanumerischen Informationen, zeitlich effektiv in kompaktes und statistisch optimales ,,Bonitätswissen'' zu überführen. Das Bonitätswissen muß zudem ,,vor Ort'' von mathematischen Laien leicht handhabbar und intuitiv verständlich sein und vom zuständigen Management des Kreditgebers mitgetragen und akzeptiert werden. Spezielle adaptive Distanzmaße erweisen sich als optimal im Sinne der Trennbarkeit ,,guter'' und ,,schlechter'' Kreditnehmer. Sie werden auch benutzt, um hochdimensionale alphanumerische und numerische Daten graphisch darzustellen. Im Vergleich mit anderen statistischen Verfahren (Fahrmeir und Hamerle (1984)) können wir auf die geringsten Fehlerraten verweisen. Die zugehörige Software XCredit läuft unter Microsoft EXCEL. Abb.1 zeigt Fehlerkurven für Trainings- und Testdaten (16795 bzw. 14745 Kunden von Mobiltelefonkarten). Jeder Kunde wird durch Informationen beschrieben, die in einer Datensatzzeile stehen:
k1,kB,kFF,k2,k1,k1,k2,k0,k0,k0,kD,k1,k2,k4,k8,k7,k1Uns ist nur die letzte Angabe je Zeile vom Inhalt her bekannt: die Klassenzuordnung. Die Fehlerraten für die Testdaten betragen 4.62 % (C4.5-Algorithmus nach Quinlan), 5.03 % (logistische Regression), 5.67 % (lineare Diskriminanzanalyse) und 4.47 % (XCredit).
k0,kS,kME,k0,k1,k1,k3,k0,k0,k0,kD,k0,k4,k1,k0,k7,k0
...
Projektliteratur: