



Bearbeiter: H. Babovsky, A. Mader
Beschreibung der Forschungsarbeit:
In der numerischen Simulation praxisrelevanter Probleme der Gasdynamik dominieren aufgrund der Komplexität nichtlinearer kinetischer Gleichungen stochastische Teilchenverfahren. Solche Algorithmen sind für Evolutionsprobleme in den letzten Jahren untersucht und mathematisch dadurch gerechtfertigt worden, daß für sie geeignete Gesetze der großen Zahlen hergeleitet werden konnten. Für stationäre Probleme hingegen fehlt eine solche Rechtfertigung, und numerische Experimente zeigen in vielen Situationen systematische Defekte. Das vorliegende Projekt konzentriert sich auf das eng umgrenzte Gebiet der stochastischen Simulation nichtlinearer eindimensionaler kinetischer Randschichten und ihrer Kopplung an strömungsdynamische Bereiche.
In [1] wurde das Verhalten stochastischer Teilchensysteme in der Nähe von Rändern systematisch untersucht. Im Vordergrund stand die Frage nach geeigneten Einström- und Reflexionsgesetzen an den physikalischen und künstlichen Rändern. Werden diese angemessen modelliert, so zeigt sich, daß außerhalb der kinetischen Randschicht die zur Herleitung der Navier-Stokes-Gleichungen benötigten Abschlußrelationen mittels Transportkoeffizienten erfüllt sind und dadurch eine Kopplung an strömungsdynamische Lösungen ermöglicht wird.

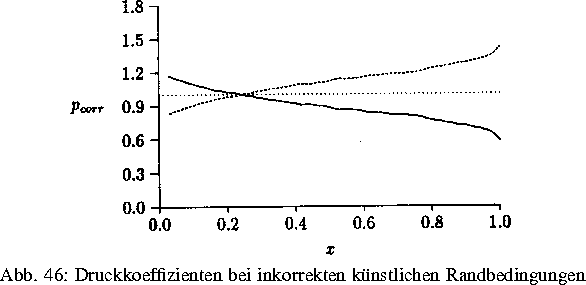
Abb. 1 zeigt die Relaxation von Koeffizienten des Drucktensors bei angemessener Behandlung des künstlichen rechten Randes im Gegensatz zur nicht angemessenen Modellierung (Abb. 2).
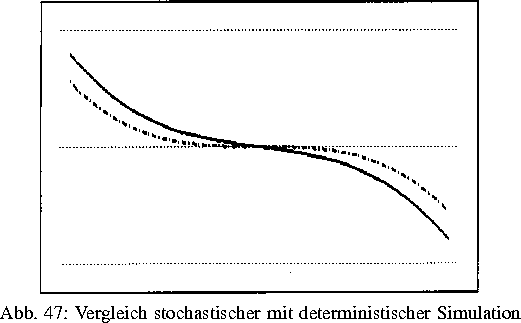
In [2] wurden deterministische Verfahren zur Behandlung von Modell-Stoßtermen der Boltzmanngleichung diskutiert, welche wesentliche Eigenschaften des Stoßoperators unverändert lassen. Die Entwicklung deterministischer Verfahren dient einmal dem Vergleich und damit der Einschätzung stochastischer Verfahren, zum anderen als Einstieg in die Entwicklung komplexerer deterministischer Algorithmen. Es ist zu erwarten, daß sich auf deterministische Verfahren moderne Diskretisierungs- und Lösungstechniken effizienter anwenden lassen als auf stochastische Simulationen. Die in Abb. 3 dargestellten Geschwindigkeitsprofile einer stationären eindimensionalen Modellströmung zeigen erhebliche Unterschiede zwischen stochastischer Simulation (durchgezogene Linie) und deterministischer Approximation (unterbrochene Linie).
Mit der Umsetzung der oben aufgeführten Ergebnisse in Algorithmen für mehrdimensionale Probleme wurde begonnen. Die Berechnung stationärer Lösungen erfolgt dabei einmal durch Relaxation des zeitabhängigen Problems, zum anderen durch Behandlung des stationären Problems als Fixpunktproblem mit einem geeigneten Iterationsverfahren.
Projektliteratur:



