[Next]:

Phase diagrams including surface tension and

[Up]:

Projects

[Previous]:

Changes of the morphology during phase

 [Contents] 

 [Index] 

Micro-macro transitions via modulation theory

Collaborator: J. Dorignac, W. Dreyer, M. Herrmann, J. Sprekels

Cooperation with: A. Mielke, J. Giannoulis (Universität Stuttgart)

Supported by: DFG: Priority Program ``Analysis, Modellbildung und Simulation von Mehrskalenproblemen'' (Analysis, modeling and simulation of multiscale problems)

Description:

This multi-scale study has the objective to derive the macroscopic laws of thermodynamics from microscopic models. A simple microscopic system is the atomic chain, which consists of N atoms with nonlinear interactions between nearest neighbors. This example looks innocent enough, however, it provides an extremely challenging task, and we are still far from the complete solution.

The dynamics of the chain is described by N > > 1 coupled ordinary differential equations of second order, which can be used to solve at any time t the positions x_$\alpha$ and the velocities $\dot{{x}}_{{\alpha}}^{}$ of the atoms $\alpha$ $\in$ {1,.., N} for given initial data. The objective is (i) to introduce a scaling parameter $\varepsilon$ = 1/N and (ii) to find admissible classes of initial data and a corresponding scaling of time and space so that in the limit $\varepsilon$ $\rightarrow$ 0, the dynamics of the chain can be described by a few partial differential equations.

Currently, the establishment of a macroscopic limit is a most contemporary issue in mathematical physics. During the period of this report, we have obtained many new partial results that exhibit the enormous difficulties of the problem.

The literature studies the scalings (i) $\bar{{t}}$ = $\varepsilon^{{3}}_{}$t, $\bar{{\alpha}}$ = $\varepsilon$($\alpha$ + ct), $\bar{{x}}$ = (1/$\varepsilon$)x, (ii) $\bar{{t}}$ = $\varepsilon^{{2}}_{}$t, $\bar{{\alpha}}$ = $\varepsilon$($\alpha$ + ct), $\bar{{x}}$ = (1/$\varepsilon$)x, where c is a constant, and considers initial data with small and smooth amplitudes. Regarding example (i), it is essential that only cold data are admissible. The resulting macroscopic equations are for (i) the Korteweg-DeVries equation and for (ii) the nonlinear Schrödinger equation. We study the hyperbolic scaling, where time, particle index, and position are scaled in the same manner: $\bar{{t}}$ = $\varepsilon$t, $\bar{{\alpha}}$ = $\varepsilon$$\alpha$, $\bar{{x}}$ = $\varepsilon$x. There results formally a 4 x 4 system of hyperbolic conservation laws for the variables specific length r, velocity $\upsilon$, wave number k, and specific entropy s:

$${\frac{{\partial r}}{{\partial\bar{t}}}} {\frac{{\partial\upsilon}}{{\partial\bar {\alpha}}}} {\frac{{\partial\upsilon}}{{\partial\bar{t}}}} {\frac{{\partial p}}{{\partial\bar{\alpha}}}} {\frac{{\partial k}}{{\partial\bar{t}}% }} {\frac{{\partial\omega}}{{\partial\bar{\alpha}}}} {\frac{{\partial s}% }{{\partial\bar{t}}}} {\frac{{\partial g}}{{\partial\bar{\alpha}}}}$$ (1)

The four variables are related to a family of four parametric traveling wave solutions of the microscopic system. In this framework, the microscopic system gives rise to an optimization problem that yields the specific energy function U(r, k, s), which is the potential for the fluxes, viz.

$${\frac{{\partial U}}{{\partial r}}} \omega {\frac{{\partial U}}{{\partial s}}} {\frac{{\partial U}}{{\partial k}}}$$ (2)

During the last period, we have studied the justification problem, i.e. the establishment of (1) and (2) as rigorous consequences of the macroscopic limit. To this end, at least two conditions must be fulfilled: 1. The system (1) with (2) constitutes a system of evolution equations. 2. Exact traveling wave solutions are stable on the microscopic scale.

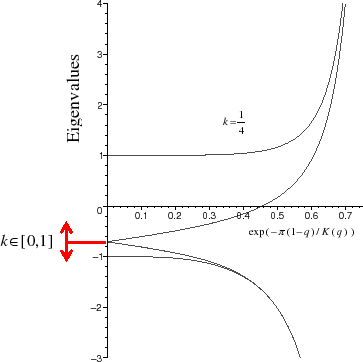
We could prove that at least for the special case that the atoms of the chain interact by means of a Toda potential, system (1) with (2) is strictly hyperbolic and genuinely nonlinear. The figure shows the four eigenvalues of the system. Stability results for traveling wave solutions are currently only available for small amplitudes. However, we have found hints that there is an intimate relation between the stability of traveling waves and the hyperbolicity of the macroscopic system, see [1, 2] for details.

Relying on these considerations, the justification problem could be solved in the high temperature limit, i.e. for hard sphere interactions. Assuming smooth solutions of (1) and (2), a rigorous proof of the macroscopic limit could be found, see [3].

References:

1. W. DREYER, M. HERRMANN, A simplification of the stability problem for periodic traveling waves in the atomic chain, Preprint no. 121, DFG Priority Program ``Analysis, Modeling and Simulation of Multiscale Problems'', Universität Stuttgart, 2004.

2. W. DREYER, M. HERRMANN, A. MIELKE, Micro-macro transition for the atomic chain via Whitham's modulation equation, Preprint no. 119, DFG Priority Program ``Analysis, Modeling and Simulation of Multiscale Problems'', Universität Stuttgart, 2004, submitted.

3. M. HERRMANN, Ein Mikro-Makro-Übergang für die nichtlineare atomare Kette mit Temperatur, PhD thesis, Humboldt-Universität zu Berlin, 2004.

[Next]:

Phase diagrams including surface tension and

[Up]:

Projects

[Previous]:

Changes of the morphology during phase

 [Contents] 

 [Index]