| - | 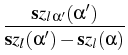 |
||
| + | (1) | ||
| (2) | |||
V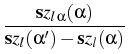 |
(3) |
|
|
|
[Contents] | [Index] |
Collaborator: W. Dreyer, F. Duderstadt, B. Wagner
Cooperation with: A. Münch (Humboldt-Universität zu Berlin, Heisenberg Fellow at WIAS), W.H. Müller (Technische Universität Berlin), T. Hauck (Motorola GmbH, München)
Supported by: DFG: Priority Program ``Analysis, Modellbildung und Simulation von Mehrskalenproblemen'' (Analysis, modeling and simulation of multiscale problems)
Description:
Under this topic, we study phase transitions that generate drastic changes of the distribution of the participating phases. In particular, we were interested in unwanted coarsening phenomena and Ostwald ripening in solder materials which are used in microelectronic devices. These phenomena are triggered by surface tension and mechanical stress deviators in the bulk. Among the investigated materials were in the past the eutectic tin/lead alloy (SnPb), which is today still the most important solder material. However, due to environmental reasons, the silver/tin (AgSn) alloy will probably substitute the SnPb alloy from next year on.
Regarding the evolution of precipitates in an eutectic SnPb alloy, we have improved the boundary integral formulation of the sharp interface limit to the phase field model.
In summary, the complete boundary integral formulation for the
evolution of the precipitates is:
| - | 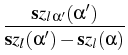 |
||
| + | (1) | ||
| (2) | |||
V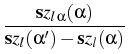 |
(3) |
This set of (integral) equations provides the normal velocity of
the interfaces ![]() for each of the interfaces
k = 1,..., N, which is then used to evolve the interface
(parametrized by
for each of the interfaces
k = 1,..., N, which is then used to evolve the interface
(parametrized by
![]() zk(
zk(![]() )) according to
)) according to
The tangential component
V![]() k of
d
k of
d![]() zk/d
zk/d![]() remains
arbitrary and a special choice of the parametrization for the
boundaries
remains
arbitrary and a special choice of the parametrization for the
boundaries ![]() will be used to simplify the numerical
implementation. As it turns out, one can find a special choice for
V
will be used to simplify the numerical
implementation. As it turns out, one can find a special choice for
V![]() k that yields the equal arclength parametrization
sk
k that yields the equal arclength parametrization
sk ![]() = Lk(
= Lk(![]() )/2
)/2![]() for all
for all ![]() , and hence
the simpler ODE-PDE system
, and hence
the simpler ODE-PDE system
|
- |
(6) |
Some first studies have appeared in [2] with just two precipitates. We also used this method to simulate the coarsening behavior of larger sets of precipitates and are presently deriving the sharp-interface model including mechanical effects for implementation into our code.
The change of the material and type of applications enforces several changes to the current model, which was originally designed to study the binary tin/lead alloy with two coexisting disordered phases.
For example, if eutectic SnPb is brought in contact with a copper plate, there results the ordered phase Cu5Sn7. An ordered phase is also present in AgSn. In both cases, the concentration variable of a binary disordered mixture is not sufficient anymore to indicate which phase is present at a local space point.
The Grinfeld instability whereupon a plane interface might become unstable if mechanical stress deviators are involved, becomes increasingly more important. We have started a study on this subject with two first objectives: (i) Establishment of a rational procedure to derive the sharp-interface equations that describe the Grinfeld instability; (ii) Examination of the influence of boundary conditions on the onset of the instability.
References:
|
|
|
[Contents] | [Index] |