Numerical aspects of unsteady incompressible non-Newtonian

[Next]:

Convective mechanisms in full-zone liquid bridges

[Up]:

Project descriptions

[Previous]:

Uniaxial, extensional flows in liquid bridges

[Contents]

[Index]

Numerical aspects of unsteady incompressible non-Newtonian flows

Collaborator: N. Scurtu

Description:

In nature, there are many fluids that do not satisfy the Newtonian constitutive law. This is also the case for many fluids created for industrial purposes. Fluids like multi-grade oils, liquid detergents, shampoos, dyes, adhesives, biological fluids like blood, paints, greases, printing inks, industrial suspensions, polymer solutions, and polymer melts, fall within the category of non-Newtonian fluids. First, the Oldroyd-A and -B fluid models are considered but the intention is to study the behavior of the generalized Oldroyd-B model, introduced by Yeleswarapu in [8], which is an up-to-date model for blood. The projected investigations could be transferred to the case of a blood-centrifuge (with bio-medical practice at the dialysis).

The numerical simulation of many industrial problems has been carried out using viscoelastic models of the Oldroyd kind. As unknowns there are the tensorial stress-field $\tau$ , the vectorial velocity-field u, and the scalar pressure-field p. The dimensionless constitutive, momentum and continuity equations for the Oldroyd model yield the following system:

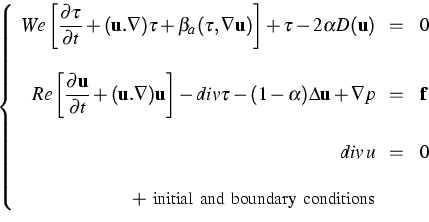
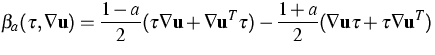$\begin{displaymath} \left \{ \begin{array} {rcl} We\left [ \displaystyle\frac{... ...mall initial and boundary conditions}} & & \end{array}\right. \end{displaymath}$

where ${\beta}_{a}(\tau,\nabla {\bf u}) = \displaystyle\frac{1-a}{2}(\tau \nabla {\b... ...tau) -\displaystyle\frac{1+a}{2}(\nabla {\bf u} \tau + \tau \nabla {\bf u}^T)$ and $a\in[-1\,,\,1]$ (a=-1 corresponding to the Oldroyd-A and a=1 to the Oldroyd-B model).

Three parameters characterize the flow: the Reynolds number $Re\geq 0$ , the fraction of viscoelastic viscosity $\alpha \in (0, 1]$ , and the Weissenberg number $We\geq 0$ . This system includes the Navier-Stokes system as a particular case (We=0), so it is favorable to develop a numerical method which can generalize an existing one used for the Navier-Stokes system.

There are two aspects which should be addressed for this system: the finite-element spatial discretization and the time discretization.

The solution of the Oldroyd problem by the finite-element method presents a difficulty due to the hyperbolic character of the constitutive equation, which is to be considered as a system in $\tau$ with ${\bf u}$ fixed (the mathematical nature of the global system is a difficult problem; loss of evolution and change of type can occur for $\alpha=1$ ). For some years the numerical solution of the Oldroyd system with convenient boundary conditions on ${\bf u}$ and $\tau$ was limited to the small Weissenberg number, because the hyperbolic character of the constitutive equation was not taken into account. This hyperbolic nature implies that some upwinding is needed. The choice of upwinding techniques depends on the choice of the finite-element space used to approximate $\tau$ . Since no continuity requirement is needed on $\tau$ at interfaces between elements, as shown in [2], this will be done by using the discontinuous Galerkin method, which allows the computation of $\tau$ on an element by element basis.

For fixed $\tau$ , the last two equations comprise a Stokes system in the variables ${\bf u}$ and p. To solve the Stokes system, a mixed finite-element method was used: the stable Taylor-Hood element was implemented on unstructured simplicial grids in 2-d and 3-d, i.e. piecewise-quadratic basis functions for the velocity and piecewise-linear for the pressure.

Major numerical problems for the unsteady Oldroyd system arise due to:

the incompressibility condition;
the strong nonlinearity in the momentum equation;
the transport of the stress;
the strong coupling of the unknowns;
stability versus accuracy of the numerical scheme.

The decoupled computation of stress, velocity, and pressure is performed with an algorithm involving a time approximation based on the fractional- $\theta$ scheme ([3]) and on the splitting method introduced by Saramito ([6]). As an operator splitting method, the $\theta$ -scheme was used by Bänsch for the Navier-Stokes equations ([1]). The method consists of splitting each time interval [t_n, t_n+1] of length $\Delta t$ into 3 subintervals $[t_{n}, t_{n}+\theta\Delta t]$ , $[t_{n}+\theta\Delta t, t_{n}+(1-\theta)\Delta t]$ , and $[t_{n}+(1-\theta)\Delta t, t_{n+1}]$ , and integrating the equations on each of these subintervals.

For the Navier-Stokes equations this scheme is 2nd order accurate, non-dissipative, and A-stable. Stability and convergence analysis of the fractional step $\theta$ -scheme for the unsteady Navier-Stokes equations are proven in [4] and [5]. Due to the complexity of the splitting method for the Oldroyd system, only the stability in the linearized case could be proven.

The splitting technique leads to three subproblems, a linear Stokes-like one, a nonlinear Burger-like one, and a stress-tensor transport problem. The first two subproblems have been solved by the finite-element methods described below and the last is in progress.

The method has been implemented in ALBERT, an adaptive finite-element toolbox ([7]).

References:

E. BÄNSCH, Simulation of instationary, incompressible flow, Acta Math., University Comenianae, LXVII (1998), pp. 101-114.
J. BARANGER, D. SANDRI, Finite element approximation of viscoelastic fluid flow: Existence of approximate solutions and error bounds, Numer. Math., 63 (1992), pp. 13-27.
R. GLOWINSKI, Numerical methods for the Navier-Stokes equations, Comput. Phys. Rep., 6 (1987), pp. 73-187.
P. KLOUCEK, F.S. RYS, Stability of the fractional step $\theta$ -schema for the nonstationary Navier-Stokes equations, SIAM J. Numer. Anal., 34 (1994), pp. 1312-1335.
S. MÜLLER-URBANIAK, Eine Analyse des Zwischenschritt- $\theta$ -Verfahrens zur Lösung der instationären Navier-Stokes-Gleichungen, Preprint 94-01, SFB 359, Ruprecht-Karls-Universität Heidelberg, 1994.
P. SARAMITO, A new $\theta$ -scheme algorithm and incompressible FEM for viscoelastic fluid flows, Math. Model. Numer. Anal., 28 (1994), pp. 1-34.
A. SCHMIDT, K.G. SIEBERT, ALBERT: An adaptive hierarchical finite element toolbox,
http://www.mathematik.uni-freiburg.de/IAM/Research/projectsdz/albert .
K.K. YELESWARAPU, M.V. KAMENEVA, K.R. RAJAGOPAL, J.F. ANTAKI, The flow of blood in tubes: Theory and experiment, Mech. Res. Commun., 25 (1998), pp. 257-262.