Optimization of curved mechanical structures

[Next]:

Research Group Dynamical Systems

[Up]:

Project descriptions

[Previous]:

Hysteresis operators in phase-field equations

[Contents]

[Index]

Optimization of curved mechanical structures

Collaborator: J. Sprekels , D. Tiba

Description:

The aim is to develop new approaches to the analysis and the optimization of curved mechanical structures like curved rods and shells . This is a continuation of the investigations on arches [1] and beams and plates [4]. Much attention is paid to the relaxation of the smoothness assumptions on the geometry of the mechanical structures.

(a) Control variational methods.

In the case of arches and plates, a new variational approach based on optimal control theory allows minimal regularity assumptions : plates with discontinuous thickness and absolutely continuous arches. In the latter case, if the tangent vector is non-zero a.e., then the classical reparametrization gives Lipschitzian representation of the arches with unit tangent vectors. It should be noted that the classical variational formulation of the Kirchhoff-Love model for arches requires three times bounded derivability of the parametrization. Moreover, the new method allows to prove the continuity and the Gâteaux/Fréchet differentiability of the mapping coefficient $\,\mapsto\,$ solution, in very weak norms. These results can be found in the papers [1], [5].

(b) Optimization of curved rods.

We are using a model that has been developed and studied, both from a theoretical and a numerical point of view, in [2]. It consists of a system of nine ordinary differential equations with null boundary conditions (the rod is clamped). Besides the deformation of the line of centroids, the cross-section may change its shape as well. The class of admissible geometries for the optimum problem is obtained by first generating the unit tangent vectors

$\begin{displaymath} \bar{t}\,=\,(\sin \varphi\, \cos \psi\,,\, \sin \varphi \, \sin \psi\,,\, \cos \varphi)\,,\end{displaymath}$

and by obtaining the parametrization via integration

$\begin{displaymath} \bar{\theta} (s)\,=\,\int\limits_0^s \bar{t} (\tau)\, d\tau\,, \quad s\,\in\,[0, L]\,.\end{displaymath}$

The given cross-section is not necessarily constant. The mappings $\varphi\,,\, \psi\,$ are in $\,C^1 (0, L)\,$ . The local frame can be obtained directly,

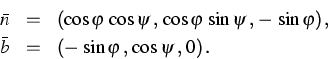
$\begin{eqnarray*} \bar{n}&=&(\cos \varphi\, \cos \psi\,,\, \cos \varphi\, \sin \... ...arphi)\,,\ \bar{b}&=&(-\, \sin \varphi\,,\, \cos \psi\,,\, 0)\,.\end{eqnarray*}$

In this way, the obtained three-dimensional curves have automatically a prescribed length $\,L\,$ , which is an essential requirement in the study of the corresponding optimal design problems. Moreover, avoiding the usage of the Frenet frame allows to consider $\,C^2 (0, L)^3\,$ -parametrizations, which is an improvement over the existing literature, where $\,C^3\,$ assumptions are required.

The examined problem consists of the minimization of a general cost functional depending on the unknown geometry $\,\bar{\theta} \in C^2 (0, L)^3\,$ and the deformation $\,\bar{y} \in H^1_0 (0, L)^9\,$

$\begin{displaymath} \hspace{6.5cm} \mbox{\rm Min} \Big\{ j (\bar{\theta}, \bar{y})\Big\}\,,\hspace{6.5cm}\mbox{\rm \bf (P)}\end{displaymath}$

under the constraint $\,\bar{\theta} \in {\cal K} \subset C^2 (0, L)^3\,$ , a closed bounded subset. Important examples are quadratic cost functionals $\,j\,$ and conditions that may be included in the definition of $\,{\cal K}\,$ :

$\begin{displaymath} 0 \, \le \, \varphi \, \le \, \frac{\pi}{2}\,-\,\varepsilon \quad \mbox{a.e. in } [0, L]\end{displaymath}$

( $\bar{\theta}\,$ has no multiple points),

$\begin{displaymath} \int\limits_0^L t_1 (\tau)\, d\tau\,=\,\int\limits_0^L t_2 (\tau)\, d\tau\,=\,0 \end{displaymath}$

(periodicity conditions for $\,\theta_1\,,\, \theta_2\,$ ), etc.

Continuity and Gâteaux differentiability with respect to $\,\varphi\,,\, \psi\,$ of the deformation $\,\bar{y}\,$ are proved in $\,C^1 (0, L)^2 \times H_0^1 (0, L)^9\,$ , equipped with the strong topologies. This allows to establish the existence of optimal shapes $\,\bar{\theta}^*\,$ for problem (P) and the writing of the first order optimality conditions. Numerical tests will be performed as well, [7].

(c) Optimization of shells.

We consider the Naghdi-type shell model introduced in [6]. It is assumed that the middle surface of the shell is the graph of a function $\,p \in C^2 (\bar{\omega})\,,\, \omega \subset \IR^2\,$ open, bounded, (multiply) connected, and the thickness is constant.

The shape optimization problem is expressed as above, by the minimization of a general cost functional depending on the geometry $\,p \in C^2 (\bar{\omega)}\,$ and on the deformation $\,\bar{y} \in H^1 (\omega)^2\,$ . Constraints of the type $\,p \in {\cal K} \subset C^2 (\bar{\omega})\,$ , closed bounded subset, may be as well imposed.

To study the continuity and the differentiability properties of the mapping $\,p \mapsto \bar{y}\,$ is very difficult, since Korn-type inequalities with constants independent of the unknown geometry $\,p\,$ are necessary. We have proved such inequalities by using an extension method. In this way, we have established the existence of at least one optimal geometry, when $\,{\cal K} \subset C^2 (\bar{\omega})\,$ is compact, and the first order optimality conditions [8]. It should be noted that the uniform Korn inequality is valid for a small enough thickness of the shell, and the uniform constants depend in a bad way on the thickness. Consequently, instabilities are to be expected in the numerical tests and special approaches are necessary.

(d) Error estimates in the discretization of control problems.

In the work [3], the above question is discussed in connection with optimal control problems governed by (elliptic) variational inequalities. In the case of convex control problems, it is known that they are equivalent with the first order system of optimality conditions. Therefore, the error estimates results valid for the finite element discretization of PDEs can be extended to optimal control problems. However, in nonconvex problems as described in the points (a), (b), (c) or in problems with constraints on the state, very little is known and high difficulties arise. The work [3] is a contribution in this respect and continues the research from [9].

References:

A. IGNAT, J. SPREKELS, D. TIBA, Analysis and optimization of nonsmooth arches, SIAM J. Control Optim., 40 (2001), pp. 1107-1135.
$\dito$ , A model of a general elastic curved rod , WIAS Preprint no. 613, 2000, to appear in: Math. Meth. Appl. Sci.
W. LIU, D. TIBA, Error estimates in the approximation of optimization problems governed by nonlinear operators, Numer. Funct. Anal. Optim., 22 (2001), pp. 953-972.
J. SPREKELS, D. TIBA, A duality approach in the optimization of beams and plates , SIAM J. Control Optim., 37 (1998/99), pp. 486-501.
$\dito$ ,Control variational methods for differential equations, in: Optimal Control of Complex Structures, K.H. Hoffmann, I. Lasiecka, G. Leugering, J. Sprekels, F. Tröltzsch, eds., vol. 139 of Internat. Series of Numerical Mathematics, Birkhäuser, Basel, 2002, pp. 245-257.
$\dito$ , An analytic approach to generalized Naghdi shell models , WIAS Preprint no. 643, 2001, to appear in : Adv. Math. Sci. Appl.
$\dito$ , Optimization problems for curved rods, in preparation.
$\dito$ ,Optimization problems for shells, in preparation.
F. TRÖLTZSCH, D. TIBA, Error estimates for the discretization of state constrained convex problems, Numer. Funct. Anal. Optim., 17 (1996), pp. 1005-1028.