Bearbeiter: A. Kunoth , S. Prößdorf , A. Rathsfeld , J. Schult
Kooperation: W. Dahmen, K. Urban (Rheinisch-Westfälische Technische Hochschule Aachen), W. Mc Lean, I. H. Sloan (University of New South Wales, Sydney)
Förderung: DFG: ,,Adaptive Multiskalenmethoden``, ,,Adaptive Multiskalenmethoden zur numerischen Behandlung von Operatorgleichungen``
Beschreibung der Forschungsarbeit:
Der Vorteil im Einsatz von Waveletmethoden in der Numerik besteht bekanntlich darin, daß man Funktionen mit lokalabhängigen Glattheitseigenschaften, wie z. B. Kernfunktionen von Integraloperatoren, gut approximieren kann, d. h. durch günstige Auswahl der Waveletbasis kann eine hohe Genauigkeit mit relativ geringer Anzahl von Freiheitsgraden erreicht werden. Für Anwendungen in der Randelementmethode bedeutet dies, daß bei der Diskretisierung der Randintegralgleichungen vollbesetzte Steifigkeitsmatrizen durch schwachbesetzte Matrizen approximiert werden können. Diese Kompressionstechnik führt zu einem schnellen Waveletalgorithmus für die Randelementmethode, der zum Gegenstand zahlreicher Veröffentlichungen avancierte.
Die wichtige Frage, welche Sorte von Wavelets für den erfolgreichen Einsatz des Algorithmus am günstigsten ist, ist aber bisher in nur ungenügendem Maße untersucht worden. Die Kompressionstechniken und Überlegungen zu den Quadraturformeln suggerieren, daß stückweise polynomiale Wavelets mit möglichst kleinem Träger die besten Kandidaten sein könnten. Diese Forderung zusammen mit der Einfachheit der Konstruktion von Wavelets im zweidimensionalen Falle führt in natürlicher Weise dazu, Multiwavelets als Ansatzfunktionen in der Randelementmethode zu betrachten. Mit anderen Worten, die Ansatzräume werden nicht mehr wie bisher definiert mittels einer hierarchischen Basis, erzeugt aus nur einer Formfunktion, sondern ein endliches System von Formfunktionen wird zur Erzeugung der hierarchischen Basis benutzt. In der Arbeit [4] wird die Approximationseigenschaft einer vollkommen allgemeinen Klasse von Multiwaveleträumen untersucht und eine wichtige Kommutatoreigenschaft (Superapproximation) bewiesen. Unter Verwendung dieser Resultate gelingt es in den Arbeiten [5,4], die Stabilität von Galerkin- und Kollokationsverfahren zur numerischen Lösung von Pseudodifferentialgleichungen durch das sogenannte numerische Symbol zu charakterisieren. Daraus ergeben sich unmittelbar neue Konvergenzeigenschaften zu den Kollokations- und Galerkinverfahren für alle wichtigen Randintegraloperatoren über glatten Randkurven. Optimale Fehlerabschätzungen können in einer entsprechenden Skala von Sobolevräumen bewiesen werden.
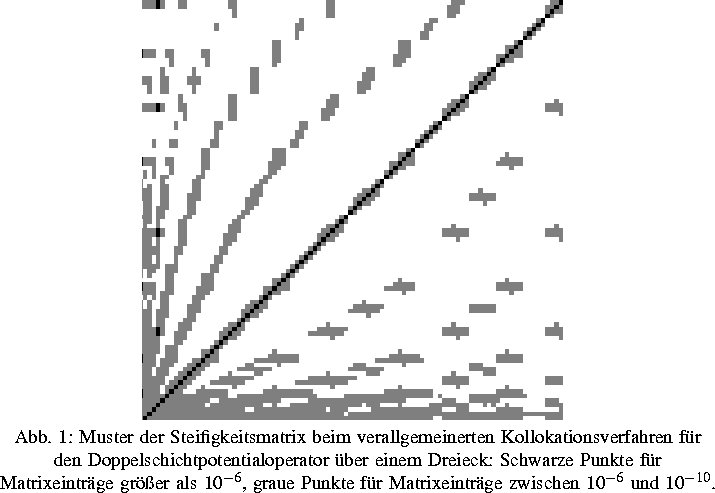
Neben der Kompression der Steifigkeitsmatrix erlauben die Waveletmethoden auch adaptive Algorithmen, bei denen die Basis des Ansatzraums durch ein ortsabhängiges Verfeinerungsniveau an die Glattheit der Lösungsfunktion angepaßt wird. Diese Methode ist der Gittergraduierung vergleichbar, gestattet aber zusätzlich, mit einer oder wenigen Formfunktionen auszukommen und die Kompressionseffekte in der Steifigkeitsmatrix beizubehalten. In der Arbeit [6] wird die stückweise lineare Kollokation für eindimensionale Randintegraloperatoren betrachtet und in natürlicher Weise ein verallgemeinertes Kollokationsverfahren mit adaptiven Ansatzräumen eingeführt. Es kann gezeigt werden, daß Stabilität und optimale Konvergenzabschätzungen erhalten bleiben. Am Beispiel des Doppelschichtoperators auf Vielecken wird demonstriert, wie die negativen Effekte, die aus der singulären Asymptotik der Lösungsfunktion resultieren, durch die günstige Wahl des Ansatzwaveletraumes kompensiert werden können. Bisher unveröffentlichte numerische Tests bestätigen die theoretischen Resultate zu Stabilität, zur Anpassung der Waveleträume und zu den Kompressionseigenschaften (vgl. Abbildung 1). Es zeigt sich sogar, daß die Stabilität wesentlich robuster ist, als die bisherige Theorie vermuten läßt.
Für die Entwicklung von Multiskalenverfahren für elliptische Randwertprobleme war die Konstruktion geeigneter Basen und deren Stabilitäts- und Konditionseigenschaften ein Schwerpunkt. In [2] wurden für diese und andere Anwendungen hinreichend allgemeine biorthogonale Wavelets auf dem Intervall konstruiert und implementiert. Über Vereinigungen parametrischer Abbildungen lassen sich dann Waveletbasen auf Mannigfaltigkeiten angeben. Weiterführend wurden in [3] quantitative Aussagen zur Stabilität der in [2] konstruierten Basen getroffen. Die Implementierung von Integralen von Wavelets wurde in bezug auf geeignete objekt-orientierte Datenstrukturen in das am IGPM, RWTH Aachen, entwickelte Softwarepaket angepaßt (vgl. [1]).
Das DFG-Projekt ,,Multiskalen-Methoden zur numerischen Behandlung von Operatorgleichungen`` wurde im Mai 1997 erfolgreich abgeschlossen.
Projektliteratur: