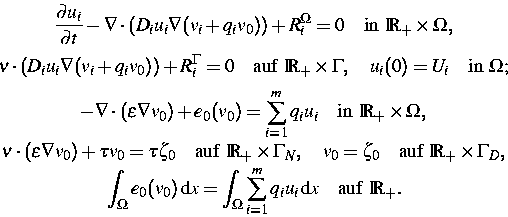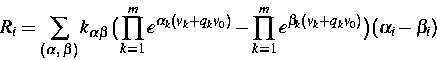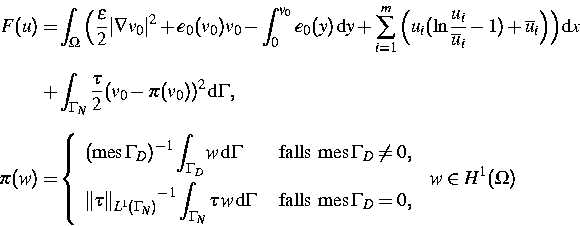Next: Stabilität von Verdichtersystemen
Up: Projektbeschreibungen
Previous: Modellierung und 2D-Simulation von Quantum-Well-Halbleiterlasern unter
Bearbeiter:
A. Glitzky
,
R. Hünlich
Kooperation: B. Heinemann, H. Rücker u. a. (Institut für
Halbleiterphysik Frankfurt (Oder) GmbH (IHP)),
N. Strecker (Institut für Integrierte Systeme, ETH Zürich)
Förderung: DFG-Sachbeihilfe
Beschreibung der Forschungsarbeit:
Wir betrachten Differentialgleichungssysteme, die die Umverteilung
elektrisch geladener Spezies in Heterostrukturen durch Diffusion und
Reaktionen unter Berücksichtigung ihrer elektrischen Wechselwirkung
modellieren, wobei wir uns bezüglich
konkreter Modelle an Problemstellungen aus der Halbleitertechnologie
orientieren (siehe auch den Beitrag auf S. ![[*]](../../1997/html/images/cross_ref_motif.gif) ).
Zunächst haben wir ein Basismodell
untersucht,
das auf ein System von
partiellen Differentialgleichungen führt,
bestehend aus Kontinuitätsgleichungen für
die Dichten aller
beteiligten beweglichen Spezies und einer linearen
Poissongleichung für das elektrostatische Potential,
wobei für die Poissongleichung gemischte Randbedingungen
anzunehmen sind [6]. Ergebnisse zu diesem Modell für den
Fall, daß nur Randbedingungen dritter Art vorliegen, haben wir auch in
[2] zusammengestellt.
).
Zunächst haben wir ein Basismodell
untersucht,
das auf ein System von
partiellen Differentialgleichungen führt,
bestehend aus Kontinuitätsgleichungen für
die Dichten aller
beteiligten beweglichen Spezies und einer linearen
Poissongleichung für das elektrostatische Potential,
wobei für die Poissongleichung gemischte Randbedingungen
anzunehmen sind [6]. Ergebnisse zu diesem Modell für den
Fall, daß nur Randbedingungen dritter Art vorliegen, haben wir auch in
[2] zusammengestellt.
In vielen Anwendungen kann das Basismodell zumindest
näherungsweise vereinfacht werden, wenn die Temperatur (wie z. B.
bei der Halbleitertechnologie-Modellierung) hoch ist.
Dann sind die kinetischen Koeffizienten
der freien Ladungsträger im Vergleich zu denen anderer Spezies sehr
groß, und
man kann
die Elektronen- und Löcherdichten aus dem Statistikansatz sowie das
elektrostatische Potential aus einer dann nichtlinearen und nichtlokalen
Poissongleichung
berechnen und somit die Kontinuitätsgleichungen für Elektronen und Löcher
weglassen.
Für die verbleibenden m Spezies mit den Ladungszahlen
qi, 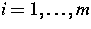 ,
bezeichnen wir mit ui, vi,
,
bezeichnen wir mit ui, vi, 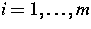 , die Konzentration und
das chemische Potential.
Das resultierende Differentialgleichungssystem umfaßt nun
m Kontinuitätsgleichungen
gekoppelt mit einer Aufgabe zur Bestimmung des chemischen und
elektrochemischen Potentials v0 und
, die Konzentration und
das chemische Potential.
Das resultierende Differentialgleichungssystem umfaßt nun
m Kontinuitätsgleichungen
gekoppelt mit einer Aufgabe zur Bestimmung des chemischen und
elektrochemischen Potentials v0 und 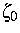 der
Elektronen, die aus einer
nichtlinearen Poissongleichung mit
gemischten Randbedingungen und mit einer nichtlokalen Nebenbedingung besteht
(zur Herleitung vgl.
[6]):
der
Elektronen, die aus einer
nichtlinearen Poissongleichung mit
gemischten Randbedingungen und mit einer nichtlokalen Nebenbedingung besteht
(zur Herleitung vgl.
[6]):
| 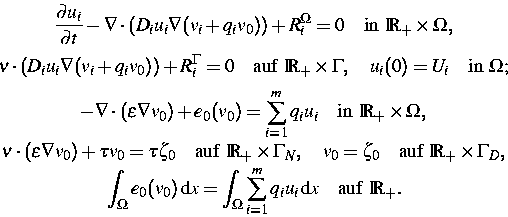 |
(1) |
Dabei sind 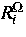 bzw.
bzw. 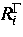 die Reaktionsraten im Volumen bzw. am
Rand, die ausgehend vom Massenwirkungsgesetz in der Form
die Reaktionsraten im Volumen bzw. am
Rand, die ausgehend vom Massenwirkungsgesetz in der Form
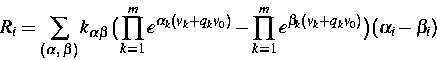
angesetzt werden. Hierbei bezeichnen 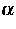 und
und 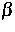 die um die
Komponenten für Elektronen und Löcher gekürzten
stöchiometrischen Vektoren der entsprechenden Reaktionen. Für den
Zusammenhang zwischen den Konzentrationen ui und
den chemischen Potentialen vi wird im betrachteten
Modell die Boltzmann-Statistik angenommen.
Die Dielektrizität
die um die
Komponenten für Elektronen und Löcher gekürzten
stöchiometrischen Vektoren der entsprechenden Reaktionen. Für den
Zusammenhang zwischen den Konzentrationen ui und
den chemischen Potentialen vi wird im betrachteten
Modell die Boltzmann-Statistik angenommen.
Die Dielektrizität 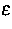 sowie die kinetischen
Koeffizienten
Di,
sowie die kinetischen
Koeffizienten
Di,
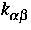 sind wegen der Heterostruktur in nichtglatter Weise
ortsabhängig, die kinetischen
Koeffizienten werden in der Regel noch vom Zustand selbst abhängen.
sind wegen der Heterostruktur in nichtglatter Weise
ortsabhängig, die kinetischen
Koeffizienten werden in der Regel noch vom Zustand selbst abhängen.
Wir beschreiben nun kurz Resultate, die wir für
eine geeignete schwache Formulierung
von (1)
gewonnen haben [4,6].
Innerhalb einer Kompatibilitätsklasse, die durch
den Anfangswert festgelegt wird, gehört zu (1)
genau ein stationärer Zustand. Das Problem
(1) besitzt höchstens eine schwache Lösung.
Entlang einer Lösung fällt die
freie Energie
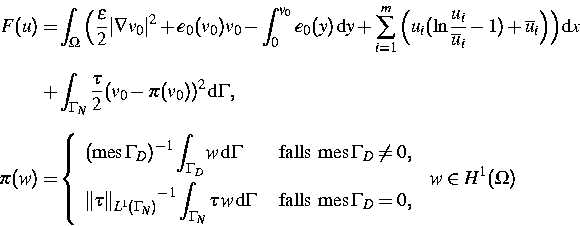
monoton. Mittels einer
Abschätzung der
freien Energie durch die Energiedissipationsrate analog zu
[3] kann
zusätzlich das exponentielle Fallen
der freien Energie entlang von Trajektorien des Systems gezeigt werden.
In [4] wird für den Fall maximal quadratischer Reaktionen im Volumen bzw.
der Ordnung eins
auf dem Rand die globale Lösbarkeit der Modellgleichungen
nachgewiesen. Zur Herleitung der nötigen a
priori-Abschätzungen werden übliche Moser-Iterationen herangezogen.
Motiviert durch Aufgaben aus der Halbleitertechnologie werden nun
spezielle Reaktionen beliebig hoher Ordnung, sogenannte
Clusterreaktionen, der Form
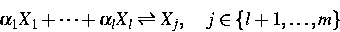
im Problem (1) zusätzlich zugelassen (vgl.
[5]).
Dabei wird angenommen, daß die Clusterspezies Xj,
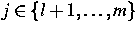 , außerdem nur an
speziellen Reaktionen maximal zweiter Ordnung
beteiligt sind.
, außerdem nur an
speziellen Reaktionen maximal zweiter Ordnung
beteiligt sind.
Die Hauptschwierigkeit bei der Behandlung von Reaktionen höherer Ordnung
liegt in den zum Nachweis der Lösbarkeit der Aufgabe erforderlichen
a priori-Abschätzungen. Wir machen wesentlichen Gebrauch von den aus dem
exponentiellen Fallen der freien Energie resultierenden Abschätzungen
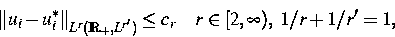
wobei ui* die Konzentrationen im stationären Zustand sind.
Zunächst starten wir mit einer möglicherweise großen Zahl von
Anlaufschritten, in denen geeignet gewählte Testfunktionen
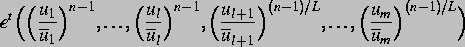
verwendet werden, die simultan
unterschiedliche Potenzen der normierten Konzentrationen für die verschiedenen
Klassen von Spezies enthalten.
Dabei bezeichnet L die maximale Ordnung aller auftretenden
Clusterreaktionen, 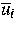 ,
, 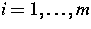 , sind
Referenzkonzentrationen.
Die Struktureigenschaften der Clusterreaktionen
gezielt ausnutzend, werden
die verwendeten Potenzen so gewählt, daß
in den Gleichungen für die
Clusterspezies Xj
die auftretenden Quellterme, die sehr hoher Ordnung sind,
mit
sehr kleinen Potenzen von
, sind
Referenzkonzentrationen.
Die Struktureigenschaften der Clusterreaktionen
gezielt ausnutzend, werden
die verwendeten Potenzen so gewählt, daß
in den Gleichungen für die
Clusterspezies Xj
die auftretenden Quellterme, die sehr hoher Ordnung sind,
mit
sehr kleinen Potenzen von 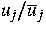 multipliziert werden.
Anschließend wird durch Moser-Iteration (nun wieder mit einheitlichen
Potenzen) die
gewünschte globale obere Schranke für Lösungen von
(1) nachgewiesen.
Globale positive untere Schranken für die Konzentrationen erhält man wie in
[4].
multipliziert werden.
Anschließend wird durch Moser-Iteration (nun wieder mit einheitlichen
Potenzen) die
gewünschte globale obere Schranke für Lösungen von
(1) nachgewiesen.
Globale positive untere Schranken für die Konzentrationen erhält man wie in
[4].
Durch Regularisierung in den Reaktionstermen wird die Aufgabe
auf endlichen Zeitintervallen in ein
Elektro-Diffusionssystem mit schwach nichtlinearen
Quelltermen im Volumen und auf dem Rand
überführt, dessen Lösbarkeit wir in [6] nachgewiesen
haben. Für dessen Lösung erhalten wir Schranken, die nicht vom
Regularisierungslevel abhängen, so daß diese Lösungen bei hinreichend
großem Abschneidelevel gleichzeitig
Lösungen von (1) sind.
Die globalen Abschätzungen für Lösungen von (1) und
das exponentielle
Fallen der freien Energie implizieren
die stärkeren asymptotischen Aussagen, daß
sich die Konzentrationen und chemischen Potentiale in jeder Lp-Norm
exponentiell ihren Gleichgewichten nähern.
Ein ähnliches
anisotropes Iterationsverfahren zum Auffinden von
a priori-Abschätzungen wie oben beschrieben
haben wir
in [1] benutzt, um ein spezielles Reaktions-Diffusionssystem
mit gewissen
Randreaktionen zweiter Ordnung
unter der Annahme der lokalen Elektroneutralität
zu behandeln.
Ergebnisse zu Zeitdiskretisierungen
der Reaktions-Diffusionsgleichungen
sind in [1,3]
enthalten.
Projektliteratur:
- A. GLITZKY, K. GRÖGER, R. HÜNLICH,
Discrete-time methods for equations modelling transport of foreign-atoms
in semiconductors, Nonlinear Anal.,
28 (1997), pp. 463-487.
- A. GLITZKY, R. HÜNLICH, Electro-reaction-diffusion systems for
heterostructures, in:
Free boundary problems and
applications (Eds. M. Niezgódka, P. Strzelecki),
Addison Wesley Longman, 1996, pp. 305-313.
- A. GLITZKY, R. HÜNLICH, Energetic estimates and asymptotics for
electro-reaction-diffusion systems, Z. Angew. Math. Mech.,
77 (1997), pp. 823-832.
- A. GLITZKY, R. HÜNLICH, Global estimates and asymptotics for
electro-reaction-diffusion systems in heterostructures,
App. Anal., 66 (1997), pp. 205-226.
- A. GLITZKY, R. HÜNLICH,
Electro-reaction-diffusion systems including cluster reactions
of higher order,
eingereicht bei: Math. Nachr.
- A. GLITZKY, R. HÜNLICH,
Electro-reaction-diffusion systems in heterostructures,
in Vorbereitung.





Next: Stabilität von Verdichtersystemen
Up: Projektbeschreibungen
Previous: Modellierung und 2D-Simulation von Quantum-Well-Halbleiterlasern unter
LaTeX typesetting by I. Bremer
1/18/1999
![[*]](../../1997/html/images/cross_ref_motif.gif) ).
Zunächst haben wir ein Basismodell
untersucht,
das auf ein System von
partiellen Differentialgleichungen führt,
bestehend aus Kontinuitätsgleichungen für
die Dichten aller
beteiligten beweglichen Spezies und einer linearen
Poissongleichung für das elektrostatische Potential,
wobei für die Poissongleichung gemischte Randbedingungen
anzunehmen sind [6]. Ergebnisse zu diesem Modell für den
Fall, daß nur Randbedingungen dritter Art vorliegen, haben wir auch in
[2] zusammengestellt.
).
Zunächst haben wir ein Basismodell
untersucht,
das auf ein System von
partiellen Differentialgleichungen führt,
bestehend aus Kontinuitätsgleichungen für
die Dichten aller
beteiligten beweglichen Spezies und einer linearen
Poissongleichung für das elektrostatische Potential,
wobei für die Poissongleichung gemischte Randbedingungen
anzunehmen sind [6]. Ergebnisse zu diesem Modell für den
Fall, daß nur Randbedingungen dritter Art vorliegen, haben wir auch in
[2] zusammengestellt.