After modelling and simulation of a technological or economical process the ultimate goal is the computation of optimal process parameters and solving problems of optimal control in this respect. In this main application area, methods of PDE-constrained optimal control, control of differential algebraic equations, and stochastic optimal control are employed in a variety of applications in technology and economy. These applications may range from basic production processes such as welding and hardening to the design of diffractive structures and simulation tasks in process engineering industry to optimal decision in financial environments such as financial (energy) derivatives, energy production and storage.
Applications in diffractive optics
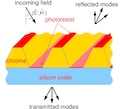
Diffractive optical elements employ the controlled use of light propagation on microstructered interfaces and can be applied in diffractive measurement technique, spectroscopy, astronomy, optical communication techniques, etc. These elements are manufactured with photolitography method, relying, in turn on precise knowledge of the optic properties of the materials. Our joint effort with the cooperation partners from PTB is in mathematical modelling and numeric simulations of the measurement process. A statistical description of the measurement result can be given as a solution of a Bayesian inverse problem. We focus on developing and applying novel methods of Bayesian inversion, stemming from optimal transport ang gradient flow theory.

Optimization Problems in Energy Management
Optimization problems in energy management are concerned with the planning of production and distribution of different energy sources (power, gas), in order to cover a given customer's demand. In this context, the consideration of uncertainties (e.g., loads, meteorological parmeters, prices) in transportation networks represents a major challenge. The aim is to find cost optimal decisions which are robust at the same time with respect to uncertainties. The additional consideration of markets and the physica of energy transport then lead to risk-averse optimal control problems with equilibrium constraints.

Simulation and optimization of industrial processes
Industrial processes are currently experiencing their fourth revolution. The entire production process is connected and equipped with sensor technology, which makes huge amounts of data available. Workers are not only supported by technical visualization and information processing, but parts of the decision-making processes are even carried out independently with the help of AI systems. The large amount of data and the fully automated process pose new challenges for mathematics, but offer unprecedented opportunities for optimization algorithms, not only in the optimization of individual production steps, but across the entire value chain.
Calibration and risk assesment of stock and interest rate models
Calibration of realistic stock and interest rate models is of prime importance. While standard interest rate products such as caps and swaptions can be priced (quasi-) analytically in a single curve Libor market model, it is impossible to match cap and swaption volatility smiles and skews observed in the markets using this model. Moreover, after the financial crisis the Libor rate could not be considered risk free anymore.
Mobile Communication Networks
Devices in our environment are increasingly networked. The exchange of data in these networks carries both opportunities and risks. Smart devices such as smartphones or self-driving cars play a special role. On the other hand, networks like the Internet of Things are made up of many simple devices. We study random mobile communication networks in terms of fundamental characteristics such as connectivity, capacity, and throughput. The focus is on the investigation of probabilities of extreme system overload, the spread of data in the network and strategies for more efficient data transmission.

Valuation of complex structured instruments in financial and energy markets
Derivatives of complex structured financial instruments with early exercise features (e.g. American style products and energy swing options) are important instruments traded at financial and energy markets. Such products give the holder the right to exercise a cash-flow or energy unit or a stream of cash-flows (energy units) at any date before expiry. For example, an investor may buy an option to swap his floating interest rates or electricity payments for example with fixed rate payments specified in the contract. Particularly for new applications in energy markets, these solutions are extended for solving problems of optimal control.