Bearbeiter: J. A. Griepentrog
Kooperation: L. Recke (Humboldt-Universität zu Berlin)
Beschreibung der Forschungsarbeit:
Gegenstand unserer Untersuchungen sind schwache Lösungen zu Randwertproblemen
für lineare elliptische Gleichungen zweiter Ordnung der Gestalt
| 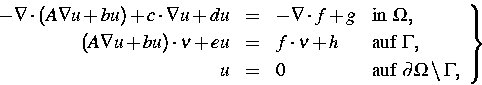 |
(1) |
wobei der Nichtglattheit der Daten des Problems eine besondere Bedeutung
zukommt.
In (1) sind 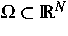 ein beschränktes
Gebiet und
ein beschränktes
Gebiet und 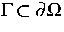 ein offenes Randstück,
so daß
ein offenes Randstück,
so daß 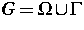 eine reguläre Menge im Sinne
von Gröger [3] darstellt.
Auf den Randstücken
eine reguläre Menge im Sinne
von Gröger [3] darstellt.
Auf den Randstücken 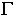 und
und 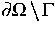 werden
gemäß (1) inhomogene, gemischte Randbedingungen gestellt.
Wir betrachten auf
werden
gemäß (1) inhomogene, gemischte Randbedingungen gestellt.
Wir betrachten auf 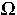 bzw.
bzw. 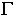 definierte,
beschränkte und meßbare Koeffizienten A, b, c, d und e,
wobei A Werte in den positiv definiten
definierte,
beschränkte und meßbare Koeffizienten A, b, c, d und e,
wobei A Werte in den positiv definiten 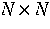 -Matrizen annimmt,
b und c vektorwertige Größen in
-Matrizen annimmt,
b und c vektorwertige Größen in 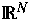 sowie d und e skalare
Größen sind.
Als Hauptresultat konnte aufbauend auf Recke [4] und
Troianiello [6], in Griepentrog, Recke [2] die Existenz
einer Konstanten
sowie d und e skalare
Größen sind.
Als Hauptresultat konnte aufbauend auf Recke [4] und
Troianiello [6], in Griepentrog, Recke [2] die Existenz
einer Konstanten 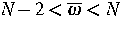 gezeigt werden,
so daß für alle Parameter
gezeigt werden,
so daß für alle Parameter
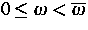 der zur schwachen Formulierung des
Problems (1) zugehörige Operator ein Fredholm-Operator
vom Index Null vom Sobolev-Campanato-Raum
der zur schwachen Formulierung des
Problems (1) zugehörige Operator ein Fredholm-Operator
vom Index Null vom Sobolev-Campanato-Raum 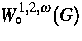 nach
nach 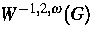 ist,
wobei die Konstante
ist,
wobei die Konstante 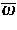 lediglich von der
Elliptizitätskonstante und von der Menge
lediglich von der
Elliptizitätskonstante und von der Menge 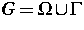 abhängt.
Darüber hinaus liegt eine lineare und stetige Abhängigkeit (im Sinne der
Operatornorm) des Fredholm-Operators von den Koeffizienten A, b, c, d
und e vor.
Verwendet wurden hierbei die Bezeichnungen
abhängt.
Darüber hinaus liegt eine lineare und stetige Abhängigkeit (im Sinne der
Operatornorm) des Fredholm-Operators von den Koeffizienten A, b, c, d
und e vor.
Verwendet wurden hierbei die Bezeichnungen
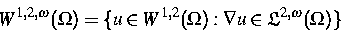
sowie
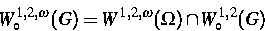
und 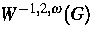 für das Bild von
für das Bild von 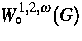 unter der Dualitätsabbildung des Raumes
unter der Dualitätsabbildung des Raumes 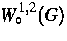 .
Aufgrund der Fredholm-Eigenschaft ergibt sich insbesondere,
daß die schwache Lösung zu Problem (1)
- falls sie eindeutig bestimmt ist - im Sinne des Sobolev-Campanato-Raumes
.
Aufgrund der Fredholm-Eigenschaft ergibt sich insbesondere,
daß die schwache Lösung zu Problem (1)
- falls sie eindeutig bestimmt ist - im Sinne des Sobolev-Campanato-Raumes
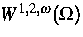 sowohl glatt von den zu folgenden Campanato-Räumen
gehörenden rechten Seiten
sowohl glatt von den zu folgenden Campanato-Räumen
gehörenden rechten Seiten
| 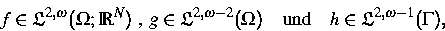 |
(2) |
als auch glatt von den Koeffizienten A, b, c, d und e im Sinne der
jeweiligen 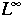 -Norm abhängt.
Man beachte, daß im Falle
-Norm abhängt.
Man beachte, daß im Falle 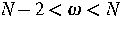 der
Sobolev-Campanato-Raum
der
Sobolev-Campanato-Raum 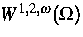 für
für 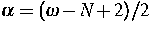 stetig
in den Hölder-Raum
stetig
in den Hölder-Raum 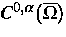 eingebettet ist.
Es handelt sich im Falle N > 2 selbst für
eingebettet ist.
Es handelt sich im Falle N > 2 selbst für 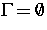 (reine Dirichlet-Randbedingungen) oder
(reine Dirichlet-Randbedingungen) oder 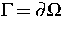 (rein natürliche Randbedingungen) um neue Ergebnisse.
Die obigen Resultate ermöglichen in dieser Raumkonstellation
interessante Anwendungen des Satzes über Implizite Funktionen
auf quasilineare elliptische Randwertprobleme mit nichtglatten Daten
(siehe Griepentrog [1] und Recke [5]).
Im Falle N = 2 folgt die glatte Abhängigkeit (im Sinne der Hölder-Norm)
der schwachen Lösungen zu Problem (1) von den Koeffizienten
(rein natürliche Randbedingungen) um neue Ergebnisse.
Die obigen Resultate ermöglichen in dieser Raumkonstellation
interessante Anwendungen des Satzes über Implizite Funktionen
auf quasilineare elliptische Randwertprobleme mit nichtglatten Daten
(siehe Griepentrog [1] und Recke [5]).
Im Falle N = 2 folgt die glatte Abhängigkeit (im Sinne der Hölder-Norm)
der schwachen Lösungen zu Problem (1) von den Koeffizienten
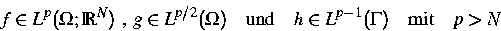
aus den Resultaten von Gröger [3].
Abschließend sei noch bemerkt, daß sich die obigen Ergebnisse auch auf den
Fall eines linearen elliptischen Systems,
dessen Hauptteil einer Dreiecksgestalt nahekommt, verallgemeinern lassen
(siehe Griepentrog, Recke [2]).
Projektliteratur:
- J. A. GRIEPENTROG, An application of the Implicit
Function Theorem to an energy model of the semiconductor theory,
Z. Angew. Math. Mech., 79 (1999), pp. 43-51.
- J. A. GRIEPENTROG, L. RECKE, Linear elliptic
boundary value problems with non-smooth data: Normal solvability on
Sobolev-Campanato spaces, WIAS-Preprint No. 446, 1998.
- K. GRÖGER, A W1,p-estimate for solutions
to mixed boundary problems for second order elliptic differential equations,
Math. Ann., 283 (1989), pp. 679-687.
- L. RECKE, Solvability properties of linear
elliptic boundary value problems with nonsmooth data, Preprint Nr. 94-3,
Fachbereich Mathematik, Humboldt-Universität zu Berlin, 1994.
-
 , Applications of the Implicit Function
Theorem to quasi-linear elliptic boundary value problems with non-smooth data,
Comm. Partial Differential Equations, 20 (1995), pp. 1457-1479.
, Applications of the Implicit Function
Theorem to quasi-linear elliptic boundary value problems with non-smooth data,
Comm. Partial Differential Equations, 20 (1995), pp. 1457-1479.
- G. M. TROIANIELLO, Elliptic Differential Equations
and Obstacle Problems, Plenum Press, New York, London, 1987.
LaTeX typesetting by I. Bremer
7/30/1999
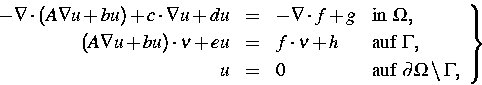
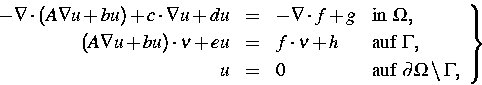
![]()
![]()
![]()