back to MMS Days 2023 Main Page »

6th Leibniz MMS Days
April 17 - April 19, 2023
Potsdam

Focus topic
Computational and Geophysical Fluid Dynamics

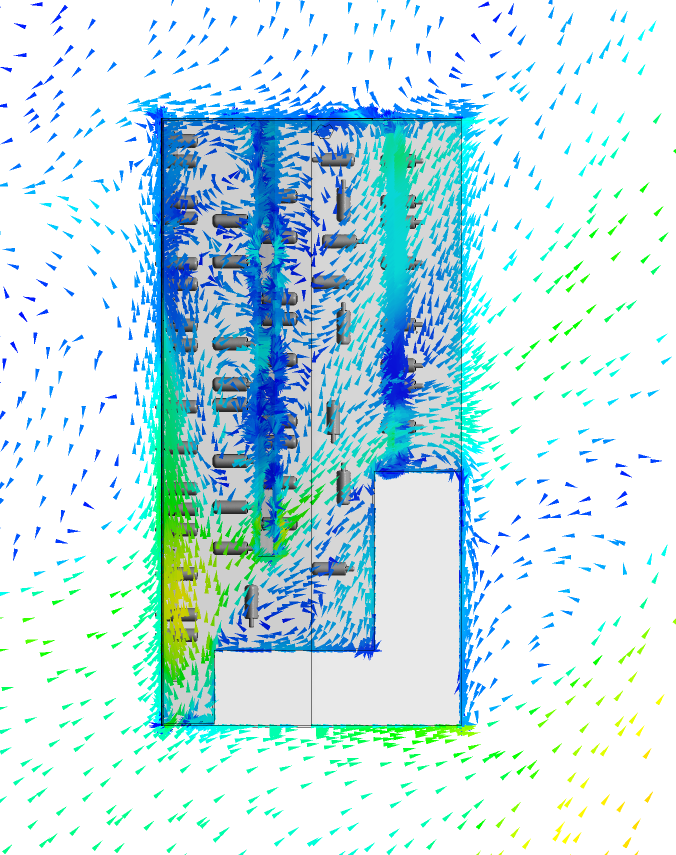
The CFD/GFD parallel session consisted of five talks with two contributions by ATB, two by TROPOS and one by WIAS. Altogether, the participants got a very good insight into different CFD applications and joint projects as well as technical aspects and difficulties in certain discretization methods. The first two talks were rather application-oriented, the last three talks were more method-oriented.

The ATB contributions were concerned with the simulation of the airflow in livestock housing systems to understand and control the indoor climate influencing the well-being of the livestock. One approach, presented by Xuefei Wu from the ATB, employed OpenFOAM with different turbulence models, while the other approach, presented by David Janke, studied the feasibility of a lattice Bolztmann method in the framework of an existing collaboration with the WIAS. Here, the open source software package OpenLB was used with the general aim to accelerate simulations for real-time application. For validation purposes the simulations were compared to experiments in the wind tunnel at ATB, which the participants also had the chance to visit during the guided tour.

The presentation by Oswald Knoth from TROPOS focussed on higher order spectral methods for advection equations implemented in the julia package CGDycore.jl, and two modifications to improve desireable structural properties like positivity and mass balance. One modification involved small constrained optimization problems, while the other modification employed a blending with a lower order finite volume method.

The other TROPOS contribution by Michael Weger presented and discussed important aspects in a multigrid approach for cut cells and block-structured Cartesian grids aimed at an efficient integration of acoustic systems.

The talk by Daniel Runge from WIAS presented an efficient reduced basis approach to solve advection-diffusion equations with nonlinear boundary conditions developed in a joint-project with the Fritz-Haber institute on heterogeneous catalysis. The approach is based on the construction of a partition of unity for the nonlinear boundary and is implemented in Julia.