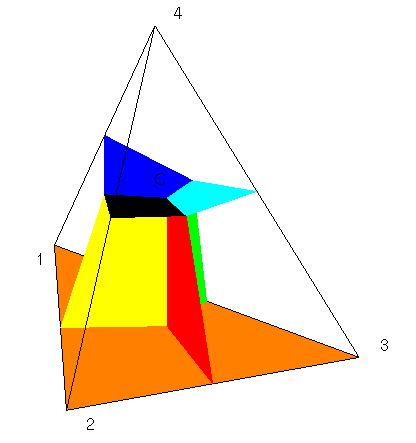
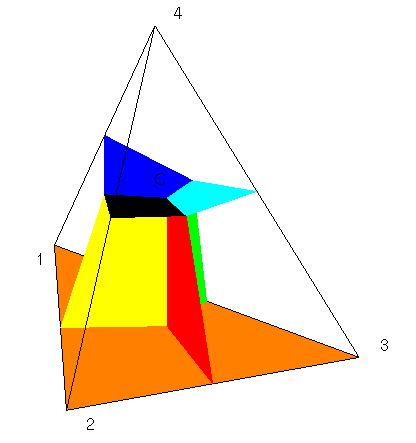
Intuitivly, this picture shows a three-dimensional simplex (a tetrahedron) with a subdivision of the tetrahedron into four disadjointed parts by selecting a point C inside it.

It is also a Delaunay tetrahedralization of a set of four points in three dimensions, which is trivial, and a Voronoi diagram of the same point set when C is the circumcenter of this tetrahedron.

More specifically, this Voronoi diagram consists of four Voronoi cells corresponding to the four points, which are all unbounded. It has six facets (shown in different colors), four edges (connecting at C) and one vertex (C).

Following are two more examples show the Voronoi diagrams corresponding to the four points when one of the four points is transformed.

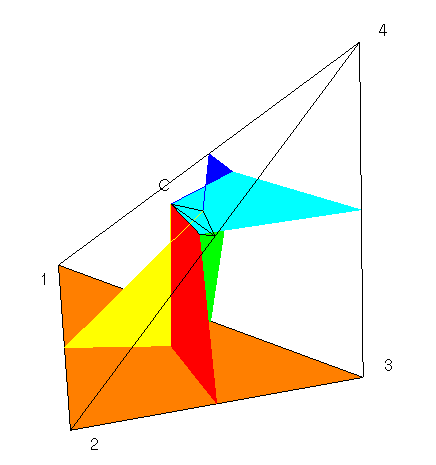
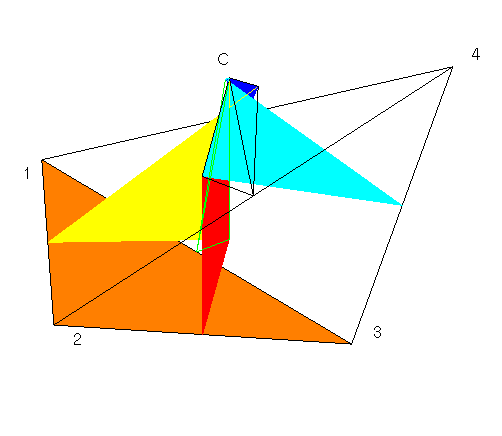
Thanks Dr. Klaus Gaertner for creating these pictures.