Numerical solution of rough and stochastic PDEs by regression techniques

Given a $d$-dimensional $\mathrm{\alpha <!--\; \alpha \; -->}$-Hölder continuous geometric rough path , $\frac{1}{3}<\mathrm{\alpha <!--\; \alpha \; -->}\le <!--\; \le \; -->\frac{1}{2}$, we aim to solve an equation of the form
$$\begin{array}{r}-<!--\; -\; -->dX=L(X)dt+\underset{k=1}{\overset{d}{\sum <!--\; \sum \; -->}}{\mathrm{\Gamma <!--\; \Gamma \; -->}}_k(X)d{\mathbf{W}}^k,X(T,\cdot <!--\; \cdot \; -->)=g,\end{array}$$where we define $$\begin{array}{r}Lf(\mathrm{\zeta <!--\; \zeta \; -->}):=\frac{1}{2}tr(\mathrm{\sigma <!--\; \sigma \; -->}(\mathrm{\zeta <!--\; \zeta \; -->})\mathrm{\sigma <!--\; \sigma \; -->}(\mathrm{\zeta <!--\; \zeta \; -->}{)}^T{D}^{2}f(\mathrm{\zeta <!--\; \zeta \; -->}))+⟨<!--\; ⟨\; -->b(\mathrm{\zeta <!--\; \zeta \; -->}),Df(\mathrm{\zeta <!--\; \zeta \; -->})⟩+c(\mathrm{\zeta <!--\; \zeta \; -->})f(\mathrm{\zeta <!--\; \zeta \; -->}),\end{array}$$ $$\begin{array}{r}{\mathrm{\Gamma <!--\; \Gamma \; -->}}_{k}f(\mathrm{\zeta <!--\; \zeta \; -->}):=⟨<!--\; ⟨\; -->{\mathrm{\beta <!--\; \beta \; -->}}_k(\mathrm{\zeta <!--\; \zeta \; -->}),Df(\mathrm{\zeta <!--\; \zeta \; -->})⟩<!--\; ⟩\; -->+{\mathrm{\gamma <!--\; \gamma \; -->}}_k(\mathrm{\zeta <!--\; \zeta \; -->})f(\mathrm{\zeta <!--\; \zeta \; -->})\end{array}$$
for a suitable test function $f:{\mathbb{R}}^n\to <!--\; \to \; -->\mathbb{R}$. Moreover, let all above functions be of suitable dimension and "smooth enough''.

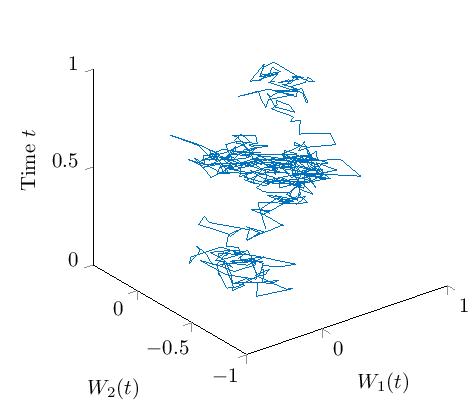
In the following, this kind of rough partial differential equation is solved numerically for a particular case. We set $c,{\mathrm{\gamma <!--\; \gamma \; -->}}_k\equiv <!--\; \equiv \; -->0$, the noise/space dimension $\mathrm{d,\; n}=2$, the terminal time $T=1$ and the terminal value $g(\mathrm{\zeta <!--\; \zeta \; -->})=\exp <!--\; \; -->\left\{-<!--\; -\; -->\frac{1}{2}{\Vert \mathrm{\zeta <!--\; \zeta \; -->}\Vert }^2\right\}$. We insert linear expressions for $\mathrm{\sigma <!--\; \sigma \; -->},b,{\mathrm{\beta <!--\; \beta \; -->}}_1,{\mathrm{\beta <!--\; \beta \; -->}}_2$ and obtain $$\begin{array}{rl}-<!--\; -\; -->dX(t,\mathrm{\zeta <!--\; \zeta \; -->})=& [\frac{1}{2}(C\mathrm{\zeta <!--\; \zeta \; -->}{)}^T{D}^{2}X(t,\mathrm{\zeta <!--\; \zeta \; -->})C\mathrm{\zeta <!--\; \zeta \; -->}+(A\mathrm{\zeta <!--\; \zeta \; -->}{)}^{T}DX(t,\mathrm{\zeta <!--\; \zeta \; -->})]dt+(N_1\mathrm{\zeta <!--\; \zeta \; -->}{)}^{T}DX(t,\mathrm{\zeta <!--\; \zeta \; -->})d{\mathbf{W}}_t^1+(N_2\mathrm{\zeta <!--\; \zeta \; -->}{)}^{T}DX(t,\mathrm{\zeta <!--\; \zeta \; -->})d{\mathbf{W}}_t^2,\\ X(1,\mathrm{\zeta <!--\; \zeta \; -->})=& g(\mathrm{\zeta <!--\; \zeta \; -->})=\exp <!--\; \; -->\left\{-<!--\; -\; -->\frac{1}{2}{\Vert \mathrm{\zeta <!--\; \zeta \; -->}\Vert }^2\right\},\end{array}$$ where $A,C,N_1,N_2$ are commuting $2\times <!--\; \times \; -->2$ matrices and $W$ is a path of a two-dimensional fractional Brownian motion with Hurst index $H=0.4$ which looks as follows
Using Feynman-Kac's formular, the above problem can be reduced to an ordinary rough differential equation since $$X(t,\mathrm{\zeta <!--\; \zeta \; -->})=\mathbb{E}g(x_1^{t,\mathrm{\zeta <!--\; \zeta \; -->}}),$$ where for $t\le <!--\; \le \; -->r\le <!--\; \le \; -->1$ the process $x_{\cdot <!--\; \cdot \; -->}^{t,\mathrm{\zeta <!--\; \zeta \; -->}}$ solves the following hybrid Stratonovich-rough differential equation: $$d{x}_r=(A-<!--\; -\; -->\frac{1}{2}{C}^2)x_{r}dt+C{x}_r\circ <!--\; \circ \; -->d{B}_r+N_1{x}_{r}d{\mathbf{W}}_r^1+N_2{x}_{r}d{\mathbf{W}}_r^2,x_t=\mathrm{\zeta <!--\; \zeta \; -->},(1)$$ where $B$ is a standard Brownian motion. Equation (1) is well-defined as a rough differential equation driven by the joint rough of $B$ and $W$.

The Feynman-Kac formular only leads to a point-wise solution of a rough partial differential equation. Therefore, we use a regression ansatz in the spatial component: $$X(t,\cdot <!--\; \cdot \; -->)\approx <!--\; \approx \; -->\stackrel{~<!--\; ~\; -->}{X}(t,\cdot <!--\; \cdot \; -->):=\underset{k=1}{\overset{K}{\sum <!--\; \sum \; -->}}{\mathrm{\kappa <!--\; \kappa \; -->}}_k(t){\mathrm{\psi <!--\; \psi \; -->}}_k(\cdot <!--\; \cdot \; -->).$$ The procedure can be visualized (for one fixed $t$) as follows:

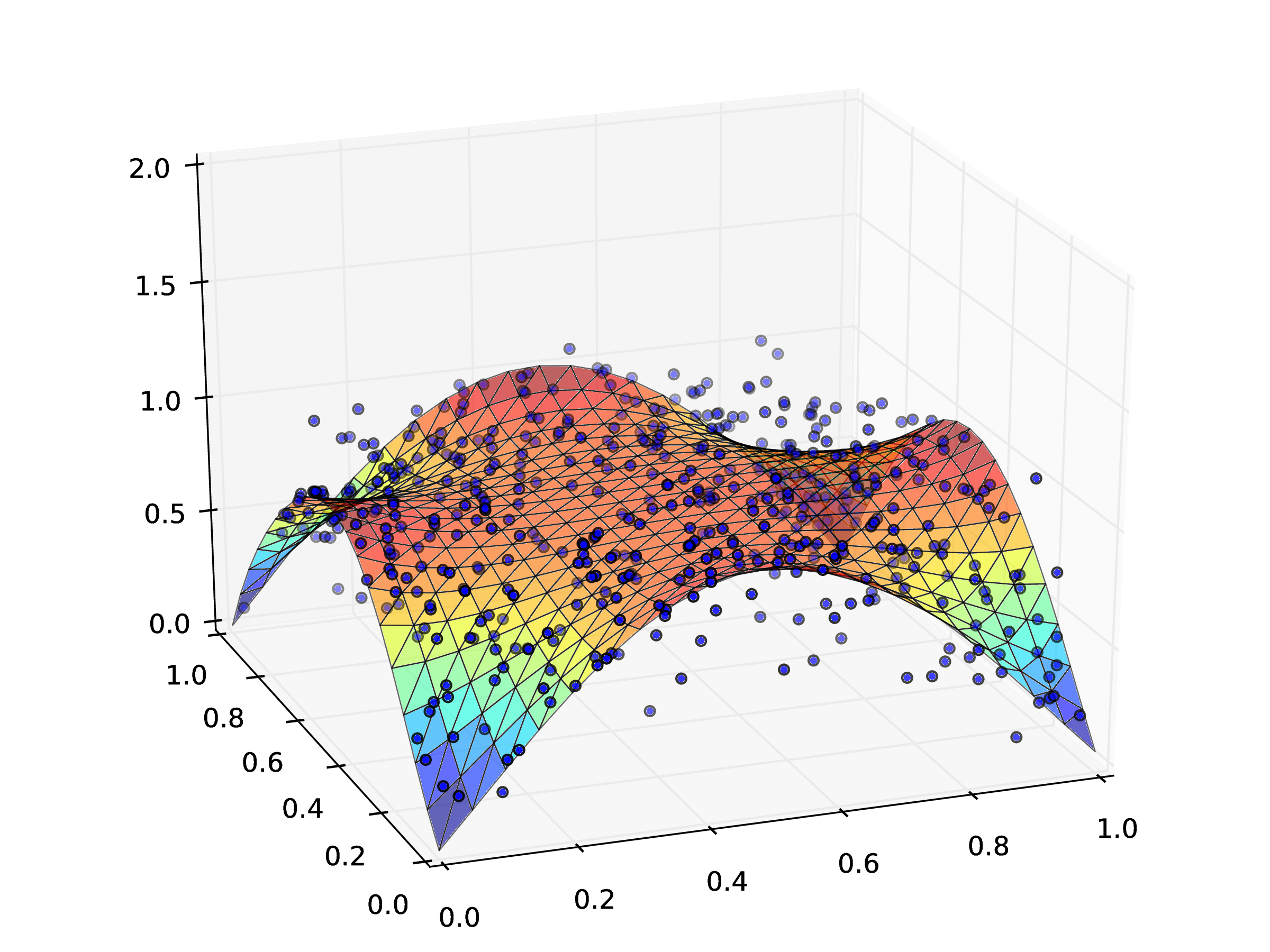
where the dots corrspond to solutions of the rough differential equation for different initial values and noise, and the and the surface corresonds to the estimated solution of the rough PDE.
We need to discretise (1) with an Euler scheme in time in order to determine the optimal coefficients ${\mathrm{\kappa <!--\; \kappa \; -->}}_1,\dots <!--\; \dots \; -->,{\mathrm{\kappa <!--\; \kappa \; -->}}_K$ for $\stackrel{~<!--\; ~\; -->}{X}$. Moreover, we sample the initial condition in (1) to have a computational efficient procedure. By doing so, we compute the regression solution on the domain $[0,1{]}^2$ for ${10}^6$ samples, a step size of $2^{-<!--\; -\; -->9}$ in the Euler scheme and $K=36$ basis functions. The regression solution is given in the following video.

In the above video the forward movement of $\stackrel{~<!--\; ~\; -->}{X}$ can be seen, i.e., if the movie is stop at a certain point, the resulting picture shows the plot of the function $\stackrel{~<!--\; ~\; -->}{X}(t,\cdot <!--\; \cdot \; -->):[0,1{]}^2\to <!--\; \to \; -->\mathbb{R}$ for a fixed time $t\in <!--\; \in \; -->[0,1]$. The x- and the y-axis represent the components ${\mathrm{\zeta <!--\; \zeta \; -->}}_1$ and ${\mathrm{\zeta <!--\; \zeta \; -->}}_2$, respectively, of the spatial variable $\mathrm{\zeta <!--\; \zeta \; -->}=({\mathrm{\zeta <!--\; \zeta \; -->}}_1,{\mathrm{\zeta <!--\; \zeta \; -->}}_2)\in <!--\; \in \; -->[0,1{]}^2$.