|
fMRI |
dMRI | |||
| close window | ||||
Functional Magnetic Resonance Imaging (fMRI)
The use structural adaptive smoothing of fMRI data leads to a significant improvement of signal detection, i.e. reduction in false positive signals, by spatially adaptive smoothing compared to a voxelwise analysis. Nonadaptive spatial smoothing can achieve a similar noise reduction only at the cost of loss of spatial information.
References: K. Tabelow, J. Polzehl, H.U. Voss, and V. Spokoiny. Analyzing fMRI experiments with structural adaptive smoothing procedures., NeuroImage 33(1), 55-62 (2006).
J. Polzehl, K. Tabelow. fmri: A package for analyzing fmri data, RNews 7(2) 13-17 (2007).
K. Tabelow, J. Polzehl, A. M. Ulug, J. P. Dyke, R. Watts, L. A. Heier, and H. U. Voss. Accurate Localization of Brain Activity in Presurgical fMRI by Structure Adaptive Smoohting, IEEE Trans. Med. Imaging 27(4), 531-537 (2008).
K. Tabelow, V. Piech, J. Polzehl, and H.U. Voss. High-resolution fMRI: Overcoming the signal-to-noise problem., Journal of Neuroscience Methods 178(2), 357-365 (2009)
J. Polzehl, K. Tabelow. Structural adaptive segmentation of statistical parametric mapping. NeuroImage 52(2), 515-523 (2010).
K. Tabelow, J. Polzehl, Statistical parametric maps for functional MRI experiments in R: The package fmri, J. Statist. Software, 44 1-21 (2011).
Introduction The aim of this paper is to offer an alternative approach for using spatial information in the statistical evaluation of fMRI experiments. fMRI data are characterized by a very low signal-to-noise ratio (SNR). Signal detection is to be performed in each voxel of a three dimensional cube. This induces a severe multiple test problem. A voxelwise analysis, using individual critical values, produces a large portion of false positive signals. At the same time small signals are concealed due to high variability of the parameter estimates. The use of a global critical value, that is, specification of an error probability to observe a false positive in any voxel, usually leads to no signal detection at all. The situation is worsened with fMRI studies aiming for ever increased resolution that is subsequently lowering the SNR.
Several methods have been proposed to enhance signal detection using spatial information present in fMRI data. This includes cluster based methods using the spatial extent of detected activations at a given threshold, together with peak intensity, to test for activations. Others involve spatial smoothing, using a Gaussian filter, with the amount of smoothing chosen to match the spatial extent of the signal to be detected. Scale space methods, attempt to achieve an optimal amount of smoothing at the expense of possible lower sensitivity. Thresholds for the tests are set by random field theory. Especially spatial smoothing employing a non-adaptive Gaussian filter trades increased detectability with loss of information on spatial extent and shape of the activation areas.
Such loss is avoided by using a spatially adaptive method, like the Propagation-Separation (PS) approach, that preserves sizes and shapes of the activated areas. In this paper we show how this method can be used in a fMRI analysis and how it improves the inferred information on the spatial extent and shape of the activated regions.
The use of such an idea, that is adaptive weights smoothing (AWS), for fMRI analysis has already been suggested. Several important questions were left open at that time. The approach was restricted to periodic activations. Furthermore it did not consider temporal and spatial correlation present in the data. And finally it failed to provide a formal solution to select appropriate thresholds for signal detection. In this paper we will overcome all these drawbacks and provide a complete procedure for structurally adaptive fMRI analysis using the PS approach.
The methodology does not use prior anatomical knowledge. Proposals in this direction can be combined with the smoothing procedures presented here.
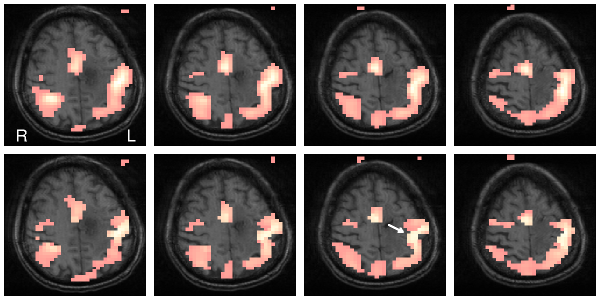
Figure 1: Upper row: Signal detection in a fMRI experiment using non-adaptive Gaussian filter in 4 subsequent slices.
Lower row: Signal detection using a structure adaptive procedure. Shape of grey matter can be seen much better (see arrow).

Figure 2: Signal detection in an artificial fMRI dataset. Left: image of a slice which is repeated in z-direction. A time series with correlated noise in space and time was added in each voxel. The greylevel corresponds to signal-to-noise ratio. Center: Result of a non adaptive analysis. Right: Result of an analysis using structure adaptive smoothing. This achieves a similar noise reduction but conserves the shape and extension of the activation areas.
|
fMRI |
dMRI | |||
| close window | ||||
last reviewed: Jan 26, 2012, K. Tabelow