| fMRI |
dMRI |
|||
| close window | ||||
Diffusion-weighted Magnetic Resonance Imaging (dMRI)
Abstract: Diffusion-weighted Magnetic Resonance Imaging (dMRI) data and Diffusion Tensor Imaging (DTI) in particular is characterized by a high noise level. Thus, estimation errors of quantities like anisotropy indices or the main diffusion direction used for fiber tracking are relatively large and may significantly confound the accuracy of DTI in clinical or neuroscience applications. Besides pulse sequence optimization, noise reduction by smoothing the data can be pursued as a complementary approach to increase the accuracy of DTI. We have suggested an anisotropic structural adaptive smoothing procedure, which is based on the Propagation-Separation method and preserves the structures seen in DTI and their different sizes and shapes.
References: K. Tabelow, J. Polzehl, V. Spokoiny, and H.U. Voss. Diffusion Tensor Imaging: Structural adaptive smoothing, NeuroImage 39(4), 1763-1773 (2007).
J. Polzehl, K. Tabelow. Structural adaptive smoothing in diffusion tensor imaging: The R package dti., Journal of Statistical Software 31, (2009).
J. Polzehl, K. Tabelow, Beyond the Gaussian model in diffussion-weighted imaging: The package dti, J. Statist. Software, 44, 1-26 (2011).
K. Tabelow, H.U. Voss, J. Polzehl, Modeling the orientation distribution function by mixtures of angular central Gaussian distributions, Journal of Neuroscience Methods 203(1) 200-211 (2012).
S. Becker, K. Tabelow, H.U. Voss, A. Anwander, R.M. Heidemann, J. Polzehl, Position-orientation adaptive smoothing of diffusion weighted magnetic resonance data (POAS), WIAS-Preprint No. 1668, (2011).
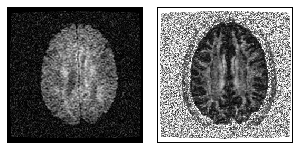
Figure 1: The left figure shows one component of the diffusion tensor, while the right figure displays the fractional anisotropy map in one slice.
Introduction Since the early times of nuclear magnetic resonance, it has been known that this phenomenon is sensitive to, and thus can be used to measure, diffusion of molecules in complex systems. The basic principles of magnetic resonance diffusion weighted imaging (DWI) were introduced in the 1980's. Since then, DWI has evolved into a versatile tool for in-vivo examination of tissues in the human brain and spinal cord, leading to a plethora of clinical and neuroscience applications. The broad interest in this technique grows from the fact that DWI probes microscopic structures well beyond typical image resolutions through water molecule displacement, which can be used in particular to characterize the integrity of neuronal tissue in the central nervous system.
Diffusion in neuronal tissue is usually not isotropic but depends on the particular microscopic structure of the tissue. Different diffusion directions can be probed by application of corresponding bipolar magnetic field diffusion gradients. In diffusion tensor imaging (DTI), this direction dependence is utilized to reveal information not only about local diffusivity but also local diffusion anisotropy, and thus, fiber structure. The information contained in a voxel of a diffusion weighted image consists of the integral of the microscopic diffusion properties over the voxel volume. In DTI, this information is reduced to a three dimensional Gaussian distribution model for diffusion. Within this model, diffusion is completely characterized by the diffusion tensor, a symmetric positive definite 3x3 matrix with six independent components. This model describes diffusion completely if the microscopic diffusion properties within a voxel are homogeneous. In the presence of partial voluming effects, like crossing fibers, the Gaussian model is only an approximation. For these cases, more sophisticated models exist, which include higher order tensors or describe non-Gaussian diffusion distributions, as used in high angular resolution diffusion imaging. In this paper, we restrict ourselves to the Gaussian diffusion tensor model for anisotropic diffusion, as used in DTI.
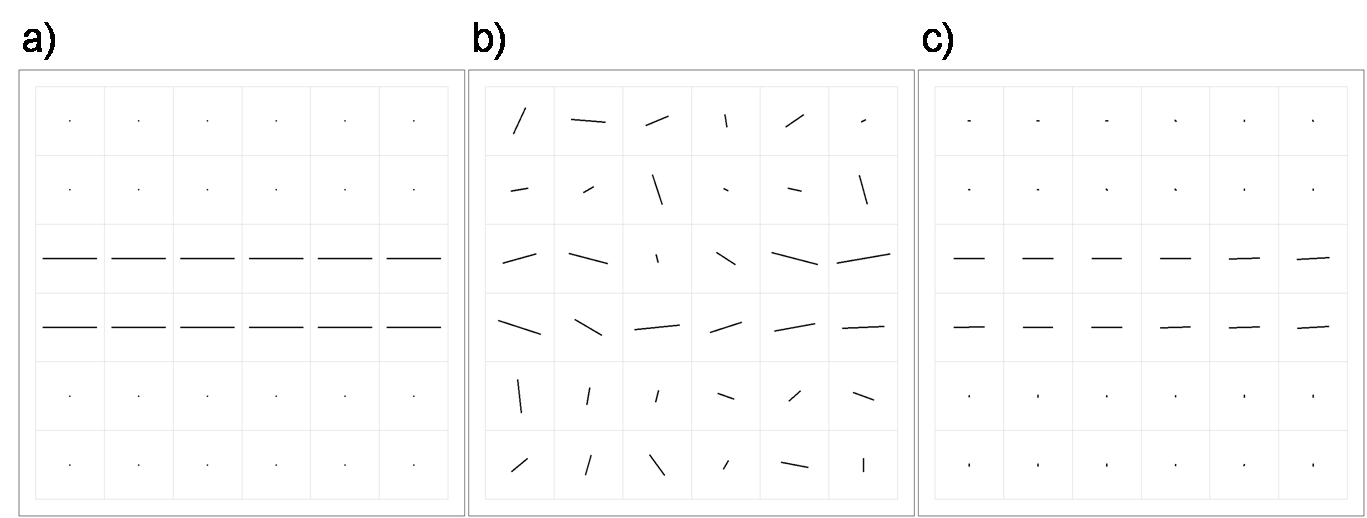
Figure 2: Effect of noise in the diffusion weighted images on the direction field of principal eigenvectors. (a) An artificial 3D DTI dataset has been created based on the direction field shown in the left figure. The direction of the lines corresponds to the direction of the direction field whereas the length of the lines corresponds to the anisotropy (FA = 0 and 0.8 for the dots and lines, respectively). One slice is shown. (b) The direction field for noisy images. Smoothing the direction field (and not the original images) can therefore only be of limited use. (c) The direction field after smoothing the original images with our proposed method.
There are several clinical and basic neuroscience applications of DTI in the human brain. Diffusion in brain white matter is highly anisotropic due to its organization into fibers of neuronal axons. DTI is able to reveal information on this fiber structure and on connections of the different regions in the brain. Fiber tracking has become an important field of interest, since it is possible to gain insight into the connections in the brain in vivo with applications such as surgical planning. In clinical or developmental studies, diffusion or anisotropy indices are usually compared by normalizing the brain volumes to a template before application of voxel-wise comparison tests. In these studies, the accuracy of diffusion and anisotropy based measures is of crucial importance, since their variability directly determines the sensitivity to detect changes over time or differences between subjects. DTI has been used in longitudinal studies and comparison of patient groups, for example in cognitive studies, developmental studies, assessment of brain injury and cancer treatment, or genetic studies. All these studies have in common that subtle changes in diffusion or anisotropy in white matter brain areas were used as an indicator for neuronal changes or differences.
DTI suffers from significant noise which may render subsequent analysis or medical decisions more difficult. This is especially important in low signal-to-noise applications, such as high-resolution DTI or DTI with high b-values. It has been shown that noise may induce a systematically biased assessment of features. For example, a well known phenomenon is the biased estimation of anisotropy indices in the presence of noise. At high noise levels, in addition to the common random errors, the order of the diffusion eigenvectors is subject to a sorting bias. Noise reduction is therefore essential. Several approaches have been proposed for smoothing diffusion tensor data. They include common methods such as Gaussian smoothing, anisotropic kernel estimates, and methods based on non-linear diffusion or splines.
Smoothing of tensor data requires to choose a Riemannian or log-Euclidian metric in the tensor space. We see some conceptional advantages in smoothing the diffusion weighted images instead of the tensor estimates. Estimating the tensor from noisy data leads, with a certain probability, to results outside the tensor space. This requires some kind of regularization. Reducing the noise level instead in the diffusion weighted images allows for a reduction of this probability in case of an underlying non-degenerate tensor. In case of high noise level in the diffusion weighted images, the non-linearity of the tensor estimation equation leads to a bias in the tensor estimate. This bias can be reduced by smoothing the diffusion weighted images, but is not addressed if smoothing is performed in the tensor space itself. A correction for Rician bias can be incorporated.
Here, we propose an alternative smoothing method based on the Propagation-Separation (PS) approach. By naturally adapting to the structures of interest at different scales, the algorithm avoids loss of information on size and shape of structures, which is typically observed when using non-adaptive filters. More specific, by virtue of inspecting scale space in an iterative way, PS accumulates information on the spatial structure at small scales and uses this information to improve estimates at coarser scales. As all spatial filters, the proposed method introduces a bias. However, this bias is controlled by the amount of achieved variance reduction.
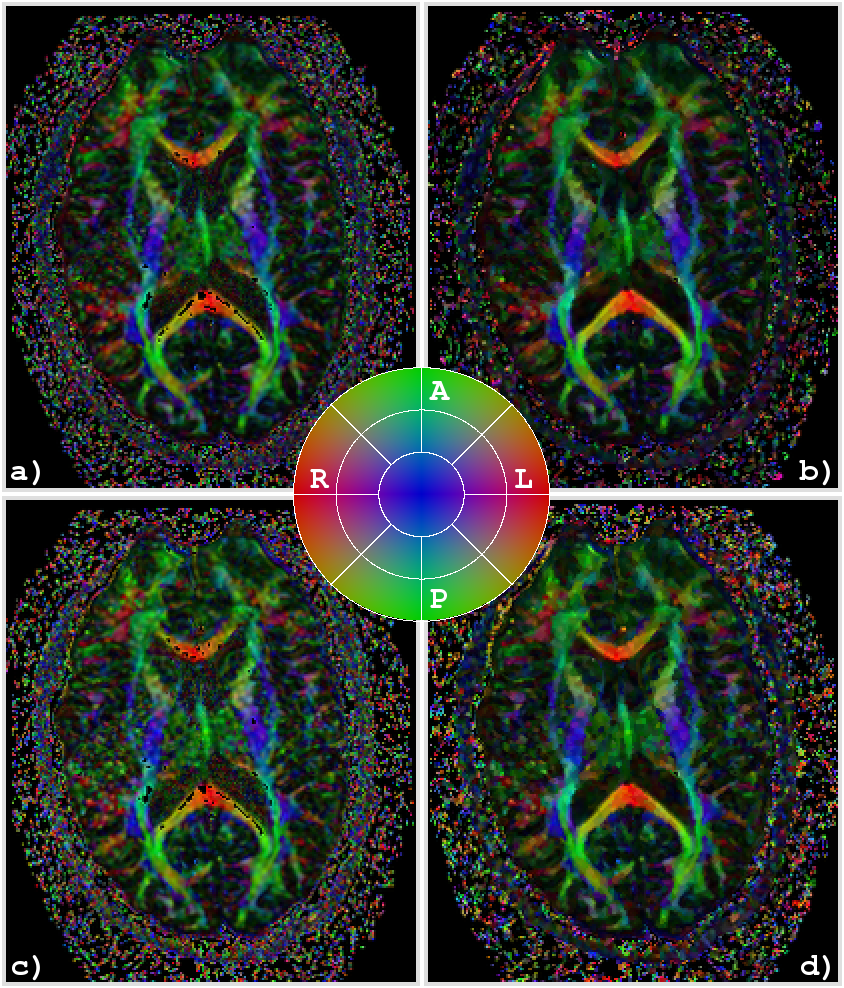
Figure 3: Application of the proposed smoothing algorithm to a brain scan: color coded directional map weighted with FA of an axial slice of the original data using all 55 diffusion weighted images (a). Directional map of the smoothed data with the procedure described in the paper with a maximal bandwith of 2.27 (b). Directional map of the original data using a reduced set of only 30 diffusion weighted images (c). Directional map of the smoothed data with only 30 diffusion weighted images (d). In all images, black regions inside the brain denote areas in which at least one of the eigenvalues was negative. The color coding is red for RL, green for AP, and blue for IS, a corresponding color map is shown in the center.
| fMRI |
dMRI |
|||
| close window | ||||
last reviewed: Jan 26, 2012, K. Tabelow