Scientific Computing, TU Berlin, WS 2019/2020, Lecture 05

Jürgen Fuhrmann, WIAS Berlin

Solution of linear systems of equations

  • Let $A$ be an $N \times N$ matrix, $b\in \mathbb R^N$.
  • Solve $Ax=b$

Direct methods

  • Exact up to machine precision (see condition number problem...)
  • Expensive (in time and space) depending on matrix properties

Iterative methods

  • "Only" approximate
  • with good convergence and proper accuracy control, results may be not worse than for direct methods
  • May be cheaper in space and (possibly) time
  • Convergence guarantee is problem dependent and can be tricky

Complexity: "big O notation"

Let $f,g: \mathbb V \to \mathbb R^+$ be some functions, where $\mathbb V=\mathbb N$ or $\mathbb V=\mathbb R$.

Write $$f(x)=O(g(x)) \quad (x\to\infty)$$ if there exist a constant $C>0$ and $x_0\in \mathbb V$ such that $$ \forall x>x_0, \quad |f(x)|\leq C|g(x)|$$

Often, one skips the part "$(x \to \infty)$"

Examples:

  • Addition of two vectors: $O(N)$
  • Matrix-vector multiplication (for matrix where all entriesre assumed to be nonzero): $O(N^2)$

Really bad example of direct method:

Solve $Ax=b$ by Cramer's rule

\begin{align*} x_i=\left| \begin{matrix} a_{11}&a_{12}&\ldots&a_{1i-1}&b_1&a_{1i+1}&\ldots&a_{1N}\\ a_{21}& &\ldots& &b_2& &\ldots&a_{2N}\\ \vdots& & & &\vdots& & &\vdots\\ a_{N1}& &\ldots& &b_N& &\ldots&a_{NN} \end{matrix}\right| / |A| \quad (i=1\dots N) \end{align*}

This takes $O(N!)$ operations...

Gaussian elimination

  • Essentially the only feasible direct solution method
  • Solve $Ax=b$ with square matrix $A$.
  • While formally, the algorithm is always the same, its implementation depends on
    • data structure to store matrix
    • possibility to ignore zero entries for matrices with many zeroes
    • sorting of elements

Pass 1

\begin{align*} \left( \begin{matrix} 6&-2 &2\\ 12&-8 &6\\ 3 &-13&3 \end{matrix}\right) x= \left(\begin{matrix} 16\\ 26\\ -19 \end{matrix}\right) \end{align*}

Step 1: $\mathrm{eqn}_2 \leftarrow \mathrm{eqn}_2-2\,\mathrm{eqn}_1$, $\mathrm{eqn}_3 \leftarrow \mathrm{eqn}_3-\frac12\,\mathrm{eqn}_1$

\begin{align*} \left(\begin{matrix} 6&-2 &2\\ 0 &-4 &2\\ 0 &-12&2 \end{matrix} \right) x= \left(\begin{matrix} 16\\ -6\\ -27 \end{matrix}\right) \end{align*}

Step 2: $\mathrm{eqn}_3 \leftarrow \mathrm{eqn}_3-3\,\mathrm{eqn}_2$ \begin{align*} \left(\begin{matrix} 6&-2 &2\\ 0 &-4 &2\\ 0 & 0&-4 \end{matrix}\right) x= \left(\begin{matrix} 16\\ -6\\ -9 \end{matrix}\right) \end{align*}

Pass 2

Solve upper triangular system \begin{align*} \left(\begin{matrix} 6&-2 &2\\ 0 &-4 &2\\ 0 &0&-4 \end{matrix}\right) x= \left(\begin{matrix} 16\\ -6\\ -9 \end{matrix}\right) \end{align*} \begin{align*} -4 x_3&= -9 &&&\Rightarrow x_3&= \frac94\\ -4 x_2 + 2 x_3 &= -6 &\Rightarrow -4 x_2 &= -\frac{21}{2} & \Rightarrow x_2&=\frac{21}{8}\\ 6x_1 -2 x_2 + 2 x_3 &= 2 &\Rightarrow 6x_1 &= 2+ \frac{21}{4}-\frac{18}{4}=\frac{11}{4} & \Rightarrow x_1&=\frac{11}{4}\\ \end{align*}

Interpretation in matrix notation

Pass 1 expressed in matrix operation \begin{align*} L_1Ax= \left(\begin{matrix} 6&-2 &2\\ 0 &-4 &2\\ 0 &-12&2 \end{matrix}\right) x&= \left(\begin{matrix} 16\\ -6\\ -27 \end{matrix}\right) =L_1 b, & L_1&= \left(\begin{matrix} 1&0&0\\ -2&1&0\\ -\frac12&0&1 \end{matrix}\right) \end{align*}\begin{align*} L_2L_1Ax= \left(\begin{matrix} 6&-2 &2\\ 0 &-4 &2\\ 0 & 0&-4 \end{matrix}\right) x&= \left(\begin{matrix} 16\\ -6\\ -9 \end{matrix}\right) =L_2L_1 b, & L_2&= \left(\begin{matrix} 1&0&0\\ 0&1&0\\ 0&-3&1 \end{matrix}\right) \end{align*}

  • Let $L=L_1^{-1}L_2^{-1}= \left(\begin{matrix} 1&0&0\\ 2&1&0\\ \frac12&3&1 \end{matrix}\right)$, $U= L_2L_1A$. Then $A=LU$
  • Inplace operation: diagonal elements of $L$ are always 1, so no need to store them $\Rightarrow$ work on storage space for $A$ and overwrite it.

LU factorization

Solve $Ax=b$:

  • Pass 1: factorize $A=LU$ such that $L,U$ are lower/upper triangular
  • Pass 2: obtain $ x=U^{-1}L^{-1}b$ by solution of lower/upper triangular systems
      1. solve $L\tilde x=b$
      1. solve $Ux=\tilde x$

A problem for LU factorization

  • Consider
$$ \left(\begin{matrix} \epsilon & 1 \\ 1 & 1 \end{matrix}\right) \left(\begin{matrix} x_1\\ x_2 \end{matrix}\right) = \left(\begin{matrix} 1+\epsilon\\2 \end{matrix}\right) $$
  • Solution: $\left(\begin{matrix} x_1\\ x_2 \end{matrix}\right) =\left(\begin{matrix} 1\\1 \end{matrix}\right)$
  • Machine arithmetic: Let $\epsilon << 1$ such that $1+\epsilon=1$.
  • Equation system in machine arithmetic: \begin{align*} 1\cdot\epsilon + 1\cdot 1 &= 1+\epsilon\\ 1\cdot 1 + 1\cdot 1 &=2 \end{align*}
In [1]:
using LinearAlgebra
ϵ=1.0e-5
A=[ϵ 1 ; 1 1]
x=[1,1]
b=[1,2]
@show A*x-b

A * x - b = [1.0000000000065512e-5, 0.0]
Out[1]:
2-element Array{Float64,1}:
 1.0000000000065512e-5
 0.0
  • Ordinary elimination: $\mathrm{eqn}_2 \leftarrow \mathrm{eqn}_2 - \frac1\epsilon \; \mathrm{eqn}_1$
$$ \left(\begin{matrix} \epsilon&1\\ 0&1-\frac1\epsilon \end{matrix}\right) \left(\begin{matrix} x_1\\ x_2 \end{matrix}\right) = \left(\begin{matrix} 1+\epsilon\\ 2-\frac{1+\epsilon}\epsilon \end{matrix}\right) $$
  • In exact arithmetic:
\begin{align*} \Rightarrow x_2=\frac{1-\frac1\epsilon}{1-\frac1\epsilon}=1 \Rightarrow x_1=\frac{1+\epsilon-x_2}\epsilon=1 \end{align*}
  • In floating point arithmetic: $1+\epsilon=1$, $1-\frac1\epsilon=-\frac1\epsilon$, $2-\frac1\epsilon=-\frac1\epsilon$:
$$ \left(\begin{matrix} \epsilon&1\\ 0&-\frac1\epsilon \end{matrix}\right) \left(\begin{matrix} x_1\\ x_2 \end{matrix}\right) = \left(\begin{matrix} 1\\ -\frac1\epsilon \end{matrix}\right) $$

$\Rightarrow$ $x_2=1$ $\Rightarrow$ $\epsilon x_1 +1 =1$ $\Rightarrow$ $x_1=0$

In [2]:
ϵ=1.0e-5
A=[ϵ 1 ; 0 1-1/ϵ]
x=[1,1]
b=[1+ϵ,2-(1+ϵ)/ϵ]
@show A*x-b;

A * x - b = [0.0, 1.4551915228366852e-11]

Partial Pivoting

  • Before elimination step, look at the element with largest absolute value in current column and put the corresponding row on top'' as thepivot''
  • This prevents near zero divisions and increases stability
$$ \left(\begin{matrix} 1&1\\ \epsilon&1 \end{matrix}\right) \left(\begin{matrix} x_1\\ x_2 \end{matrix}\right) = \left(\begin{matrix} 2\\1+\epsilon \end{matrix}\right) \Rightarrow \left(\begin{matrix} 1&1\\ 0&1-\epsilon \end{matrix}\right) \left(\begin{matrix} x_1\\ x_2 \end{matrix}\right) = \left(\begin{matrix} 2\\ 1-\epsilon \end{matrix}\right) $$
  • Independent of $\epsilon$: \begin{align*} x_2=\frac{1-\epsilon}{1-\epsilon}=1,\qquad x_1=2-x_2=1 \end{align*}
In [3]:
ϵ=1.0e-5
A=[1 1 ; 0 1-ϵ]
x=[1,1]
b=[2,1-ϵ]
@show A*x-b;

A * x - b = [0.0, 0.0]
  • Instead of $A$, factorize $PA$: $PA=LU$, where $P$ is a permutation matrix which can be encoded using an integer vector

How does Julia handle the LU factorization ?

In [4]:
ϵ=1.0e-5
A=[ϵ 1 ; 1 1]
b=[1,2]
x=A\b
@show x;
@show A*x-b;

x = [1.000010000100001, 0.9999899998999989]
A * x - b = [-1.1102230246251565e-16, 0.0]

It seems it does something right ...

In [5]:
Alu=lu(A)
LxU=Alu.L*Alu.U
@show LxU
@show LxU[Alu.p,:]
@show Alu.p

LxU = [1.0 1.0; 1.0e-5 1.0]
LxU[Alu.p, :] = [1.0e-5 1.0; 1.0 1.0]
Alu.p = Int32[2, 1]
Out[5]:
2-element Array{Int32,1}:
 2
 1
  • The LU factorization object has three components: L, U, and p: the two factors and the pivot table

Gaussian elimination and LU factorization

  • Full pivoting: in addition to row exchanges, perform column exchanges to ensure even larger pivots. Seldomly used in practice.
  • Gaussian elimination with partial pivoting is the "working horse" for direct solution methods
  • Complexity of LU-Factorization: $O(N^3)$, some theoretically better algorithms are known with e.g. $O(N^{2.736})$
  • Complexity of triangular solve: $O(N^2)$ $\Rightarrow$ overall complexity of linear system solution is $O(N^3)$
  • Cholesky factorization: $A=LL^T$ for symmetric, positive definite matrices

Implementation

  • Due to multiple dispatch Julia chooses the best implementation for a given data type
  • Generic variant for any number typpe

  • BLAS, LAPACK for Float32, Float64

    • BLAS: Basic Linear Algebra Subprograms (http://www.netlib.org/blas/)

      • Level 1 - vector-vector: $\mathbf{y} \leftarrow \alpha \mathbf{x} + \mathbf{y}$
      • Level 2 - matrix-vector: $\mathbf{y} \leftarrow \alpha A \mathbf{x} + \beta \mathbf{y}$
      • Level 3 - matrix-matrix: $C \leftarrow \alpha A B + \beta C$

    • LAPACK: Linear Algebra PACKage (http://www.netlib.org/lapack/)

      • Linear system solution, eigenvalue calculation etc.
      • dgetrf: LU factorization
      • dgetrs: LU solve

    • Used in overwhelming number of codes (e.g. matlab, scipy etc.). Also, C++ matrix libraries use these routines. Unless there is special need, they should be used.

    • Reference implementations in Fortran, but many more implementations available which carefully work with cache lines etc.

Matrices from Partial Differential Equations (PDEs)

  • So far, we assumed that matrices are stored in a two-dimensional, $N\times N$ array of numbers
  • This kind of matrix storage are also called dense
  • As we will see, matrices from PDEs (can) have a number of structural properties one can take advantage of when storing a matrix and solving the linear system

1D heat conduction

  • $v_L, v_R$: ambient temperatures, $\alpha$: heat transfer coefficient
  • Second order boundary value problem in $\Omega=[0,1]$: \begin{align*} -u''(x)&=f(x) &\text{in} \Omega\\ -u'(0) + \alpha (u(0) - v_L)&=0\\ u'(1) + \alpha (u(1) - v_R)&=0 \end{align*}
  • Let $h=\frac1{N-1}$, $x_i=x_0+(i-1)h$ ($i=1\dots n$) be discretization points, let $u_i$ approximations for $u(x_i)$ and $f_i=f(x_i)$
  • Finite difference approximation: \begin{align*} -u'(0) +\alpha (u(0) - v_L) &\approx \frac{1}{h}(u_{0}-u_1) + \alpha (u_0 - v_L) \\ -u''(x_i)-f(x_i) &\approx \frac{1}{h^2}(-u_{i+1}+2u_i- u_{i-1})-f_i & (i=2\dots N-1)\\ u'(1) + \alpha (u(1) - v_R) &\approx \frac{1}{h}(u_{N}-u_{N-1})+ \alpha (u_N - v_R)\\ \end{align*}

1D heat conduction: discretization matrix}

  • equations $2\dots N-1$ multiplied by $h$
  • only nonzero entries written
\begin{align*} \left(\begin{matrix} \alpha+\frac1h & -\frac1h & & & \\ -\frac1h & \frac2h & -\frac1h & &\\ & -\frac1h & \frac2h & -\frac1h &\\ & \ddots & \ddots & \ddots & \ddots\\ & & -\frac1h & \frac2h & -\frac1h & \\ & & & -\frac1h & \frac2h & -\frac1h \\ & && & -\frac1h & \frac1h + \alpha \end{matrix}\right) \left( \begin{matrix} u_1 \\ u_2 \\ u_3 \\\vdots \\ u_{N-2} \\ u_{N-1} \\ u_{N} \end{matrix} \right) = \left( \begin{matrix} \alpha v_L \\ hf_2 \\ hf_3 \\\vdots \\ hf_{N-2} \\ hf_{N-1} \\ \alpha v_R \end{matrix} \right) \end{align*}
  • Each row contains $\leq 3$ elements
  • Only $3N-2$ of $N^2$ elements are non-zero

General tridiagonal matrix

\begin{align*} \left(\begin{matrix} {b_1} & {c_1} & { } & { } & { } \\ {a_2} & {b_2} & {c_2} & { } & { } \\ { X} & {a_3} & {b_3} & \ddots & { } \\ { } & { } & \ddots & \ddots & {c_{n-1}}\\ { } & { } & { } & {a_N} & {b_N}\\ \end{matrix}\right) \left(\begin{matrix} {u_1 } \\ {u_2 } \\ {u_3 } \\ \vdots \\ {u_N } \\ \end{matrix}\right) = \left(\begin{matrix} {f_1 } \\ {f_2 } \\ {f_3 } \\ \vdots \\ {f_N } \\ \end{matrix}\right) \end{align*}
  • To store matrix, it is sufficient to store only nonzero elements in three one-dimensional arrays for $a_i, b_i, c_i$, respectively

Gaussian elimination for tridiagonal systems

Gaussian elimination using arrays $a,b,c$ as matrix storage ?

  • From what we have seen, this question arises in a quite natural way, and historically, the answer has been given several times and named differently
    • TDMA (tridiagonal matrix algorithm)
    • "Thomas algorithm" (Llewellyn H. Thomas, 1949 (?))
    • "Progonka method" (from Russian "progonka" "run through"; Gelfand, Lokutsievski, 1952, published 1960)

Progonka: derivation

  • $a_i u_{i-1} + b_i u_i + c_i u_{i+1} = f_i \quad (i=1\dots N)$; $a_1=0$, $c_N=0$
  • For $i=1\dots N-1$, assume there are coefficients $\alpha_i, \beta_i$ such that $u_i=\alpha_{i+1}u_{i+1}+\beta_{i+1}$.
  • Then, we can express $u_{i-1}$ and $u_{i}$ via $u_{i+1}$: $$(a_i\alpha_i\alpha_{i+1}+ b_i \alpha_{i+1} + c_i) u_{i+1} + a_i\alpha_i\beta_{i+1}+ a_i\beta_i +b_i \beta_{i+1} -f_i=0$$
  • This is true independently of $u$ if
\begin{align*} \begin{cases} a_i\alpha_i\alpha_{i+1}+ b_i \alpha_{i+1} + c_i&=0\\ a_i\alpha_i\beta_{i+1}+ a_i\beta_i +b_i \beta_{i+1} -f_i &=0 \end{cases} \end{align*}
  • or for $i=1\dots N-1$:
\begin{align*} \begin{cases} \alpha_{i+1}&= -\frac{c_i}{a_i\alpha_i+b_i}\\ \beta_{i+1} &= \frac{f_i - a_i\beta_i}{a_i\alpha_i+b_i} \end{cases} \end{align*}

Progonka: realization

  • Initialization: $\begin{cases} \alpha_{2}&= -\frac{c_1}{b_1}\\ \beta_{2} &= \frac{f_i}{b_1} \end{cases}$

  • Forward sweep: for $i=2\dots N-1$: $\begin{cases} \alpha_{i+1}&= -\frac{c_i}{a_i\alpha_i+b_i}\\ \beta_{i+1} &= \frac{f_i - a_i\beta_i}{a_i\alpha_i+b_i} \end{cases}$

  • $u_N=\frac{f_N - a_N\beta_N}{a_N\alpha_N+b_N}$

  • Backward sweep: for $i= N-1 \dots 1$: $u_i=\alpha_{i+1}u_{i+1}+\beta_{i+1}$

Прогонка: properties

  • $n$ unknowns, one forward sweep, one backward sweep $\Rightarrow$ $O(N)$ operations vs. $O(N^3)$ for algorithm using full matrix
  • No pivoting $\Rightarrow$ stability issues
  • Stability for diagonally dominant matrices ($|b_i| > |a_i| + |c_i|$)
  • Stability for symmetric positive definite matrices

Progonka: Julia

Diagonally dominant matrix

In [6]:
N=5
a=[0.1 for i=1:N-1]
b=[0.5 for i=1:N]
c=[0.1 for i=1:N-1]
A=Tridiagonal(a,b,c)
Alu=lu(A)
@show Alu.p
@show Alu.L*Alu.U
rhs=[1.0 for i=1:N]
x=A\rhs
@show A*x-rhs

Alu.p = Int32[1, 2, 3, 4, 5]
Alu.L * Alu.U = [0.5 0.1 0.0 0.0 0.0; 0.1 0.5 0.1 0.0 0.0; 0.0 0.1 0.5 0.1 0.0; 0.0 0.0 0.1 0.5 0.1; 0.0 0.0 0.0 0.1 0.5]
A * x - rhs = [0.0, 0.0, -1.1102230246251565e-16, 0.0, 0.0]
Out[6]:
5-element Array{Float64,1}:
  0.0                   
  0.0                   
 -1.1102230246251565e-16
  0.0                   
  0.0

Random matrix $\Rightarrow$ pivoting

In [7]:
a=randn(N-1)
b=randn(N)
c=randn(N-1)
A=Tridiagonal(a,b,c)
Alu=lu(A)
@show Alu.p
@show Alu.L*Alu.U
rhs=[1.0 for i=1:N]
x=A\rhs
@show A*x-rhs

Alu.p = Int32[1, 2, 4, 5, 3]
Alu.L * Alu.U = [1.642209664435775 -0.4061308256034484 0.0 0.0 0.0; 1.1763362225664113 0.8365867169691616 0.46225054455226755 0.0 0.0; 0.0 0.0 0.8968790408954165 0.025878505187374626 0.1769613752212565; 0.0 0.0 0.0 1.3036311837751307 -0.9631535613011202; 0.0 0.2839556221361067 -0.593810878253905 0.6154455894919252 0.0]
A * x - rhs = [0.0, -1.1102230246251565e-16, 0.0, 0.0, 2.220446049250313e-16]
Out[7]:
5-element Array{Float64,1}:
  0.0                   
 -1.1102230246251565e-16
  0.0                   
  0.0                   
  2.220446049250313e-16

used dgtrsv from LAPACK

2D Rectangular discretization grid

  • Each discretization point has not more then 4 neighbours
  • Matrix can be stored in five diagonals, LU factorization not anymore $\equiv$ "fill-in"
  • Certain iterative methods can take advantage of the regular and hierachical structure (multigrid) and are able to solve system in $O(N)$ operations
  • Another possibility: fast Fourier transform with $O(N\log N)$ operations

Sparse matrices

  • Tridiagonal and five-diagonal matrices can be seen as special cases of sparse matrices
  • Generally they occur in finite element, finite difference and finite volume discretizations of PDEs on structured and unstructured grids
  • Definition: Regardless of number of unknowns $N$, the number of non-zero entries per row remains limited by $n_r$
  • If we find a scheme which allows to store only the non-zero matrix entries, we would need $Nn_r= O(N)$ storage locations instead of $N^2$
  • The same would be true for the matrix-vector multiplication if we program it in such a way that we use every nonzero element just once: matrix-vector multiplication would use $O(N)$ instead of $O(N^2)$ operations

Sparse matrix formats

  • What is a good storage format for sparse matrices?
  • Is there a way to implement Gaussian elimination for general sparse matrices which allows for linear system solution with $O(N)$ operation ?
  • Is there a way to implement Gaussian elimination \emph{with pivoting} for general sparse matrices which allows for linear system solution with $O(N)$ operations?
  • Is there any algorithm for sparse linear system solution with $O(N)$ operations?

Coordinate (triplet) format

  • Store all nonzero elements along with their row and column indices
  • One real, two integer arrays, length = nnz= number of nonzero elements Y.Saad, Iterative Methods, p.92}

Compressed Row Storage (CRS) format}

(aka Compressed Sparse Row (CSR) or IA-JA etc.)

  • real array AA, length nnz, containing all nonzero elements row by row
  • integer array JA, length nnz, containing the column indices of the elements of AA
  • integer array IA, length N+1, containing the start indizes of each row in the arrays IA and JA and IA[N+1]=nnz+1 \begin{align*} A&= \left(\begin{matrix} 1.& 0. & 0.& 2.& 0.\\ 3.& 4. & 0.& 5.& 0.\\ 6.& 0. & 7.& 8.& 9.\\ 0.& 0. & 10.& 11. & 0.\\ 0.& 0. & 0.& 0.& 12. \end{matrix}\right)\\ \end{align*}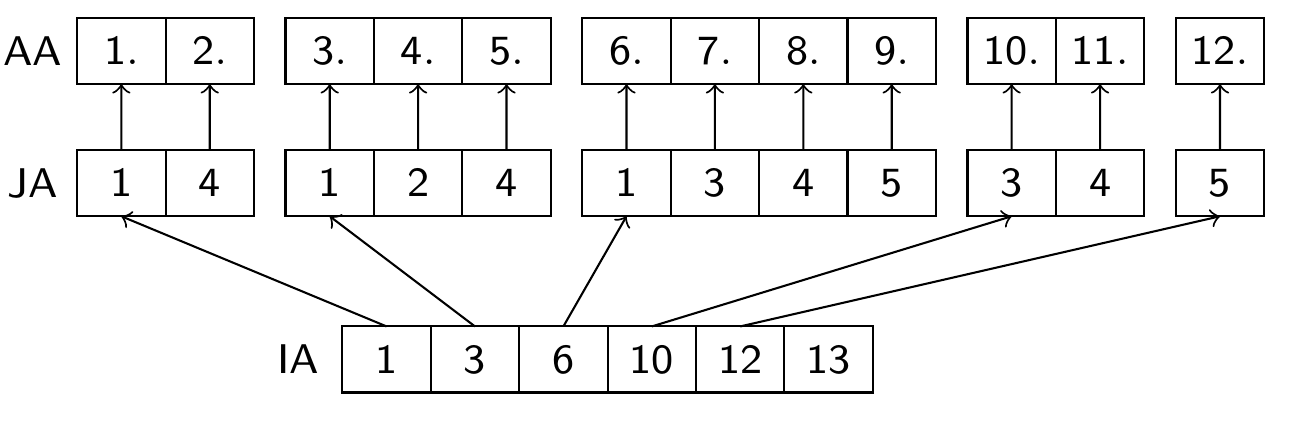
  • Used in most sparse matrix solver packages
  • CSC (Compressed Column Storage) uses similar principle but stores the matrix column-wise. Used in Julia

Sparse direct solvers

  • Sparse direct solvers implement Gaussian elimination with different pivoting strategies
  • UMFPACK: Used in Julia
  • Pardiso (omp + MPI parallel)
  • SuperLU (omp parallel)
  • MUMPS (MPI parallel)
  • Pastix
  • Quite efficient for 1D/2D problems
  • Essentially they implement the LU factorization algorithm
  • They suffer from fill-in, especially for 3D problems: Let $A=LU$ be an LU-Factorization. Then, as a rule, $nnz(L+U) > nnz(A)$.
  • $\Rightarrow$ increased memory usage to store L,U
  • $\Rightarrow$ high operation count

Sparse direct solvers: solution steps (Saad Ch. 3.6)

  1. Pre-ordering
    • Decrease amount of non-zero elements generated by fill-in by re-ordering of the matrix
    • Several, graph theory based heuristic algorithms exist
  2. Symbolic factorization
    • If pivoting is ignored, the indices of the non-zero elements are calculated and stored
    • Most expensive step wrt. computation time
  3. Numerical factorization
    • Calculation of the numerical values of the nonzero entries
    • Moderately expensive, once the symbolic factors are available
  4. Upper/lower triangular system solution
    • Fairly quick in comparison to the other steps
  • Separation of steps 2 and 3 allows to save computational costs for problems where the sparsity structure remains unchanged, e.g. time dependent problems on fixed computational grids
  • With pivoting, steps 2 and 3 have to be performed together, and pivoting can increase fill-in
  • Instead of pivoting, iterative refinement may be used in order to maintain accuracy of the solution

Sparse direct solvers: influence of reordering

  • Sparsity patterns for original matrix with three different orderings of unknowns
    • number of nonzero elements (of course) independent of ordering: 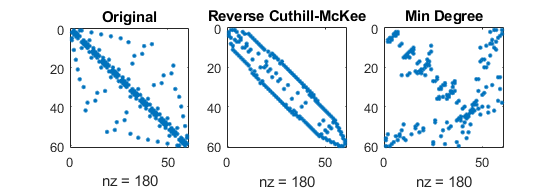(mathworks.com)
  • Sparsity patterns for corresponding LU factorizations
    • number of nonzero elements depend original ordering! 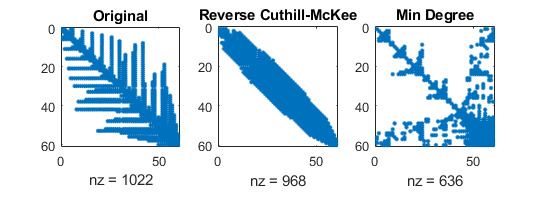(mathworks.com)

Sparse direct solvers: Complexity estimate

  • Complexity estimates depend on storage scheme, reordering etc.
  • Sparse matrix - vector multiplication has complexity $O(N)$
  • Some estimates can be given from graph theory for discretizations of heat equation with $N=n^d$ unknowns on close to cubic grids in space dimension $d$
  • sparse LU factorization:
\begin{align*} \begin{array}{ccc} d & work & storage\\ \hline 1 & O(N) \;|\; O(n) & O(N)\;|\;O(n)\\ 2 & O(N^{\frac32}) \;|\; O(n^3) & O(N\log N) \;|\; O(n^2\log n)\\ 3& O(N^2)\;|\; O(n^6) & O(N^{\frac43})\;|\; O(n^4) \end{array} \end{align*}
  • triangular solve: work dominated by storage complexity
\begin{align*} \begin{array}{cc} d & work\\ \hline 1 & O(N)\;|\;O(n)\\ 2 & O(N\log N) \;|\; O(n^2\log n)\\ 3 & O(N^{\frac43})\;|\; O(n^4) \end{array} \end{align*}

(Source: J. Poulson, PhD thesis, http://hdl.handle.net/2152/ETD-UT-2012-12-6622)

Julia code

In [8]:
using SparseArrays
N=100
A=sprand(N,N,0.5) # random matrix with probaility 0.5 that $A_{ij}$ is nonzero
Alu=lu(A)
@show Alu.p
b=ones(N)
x=A\b
@show norm(A*x-b)

Alu.p = [21, 30, 65, 26, 67, 16, 28, 72, 95, 89, 31, 42, 8, 84, 87, 45, 39, 6, 1, 100, 3, 79, 40, 22, 15, 49, 20, 59, 35, 29, 52, 55, 69, 11, 27, 62, 66, 99, 97, 68, 38, 36, 80, 32, 75, 14, 54, 86, 73, 37, 48, 61, 71, 81, 58, 77, 82, 24, 88, 17, 91, 5, 90, 93, 85, 43, 2, 23, 34, 78, 9, 51, 64, 74, 98, 70, 33, 83, 13, 7, 53, 47, 50, 46, 12, 57, 56, 4, 25, 63, 76, 96, 19, 92, 94, 10, 60, 41, 44, 18]
norm(A * x - b) = 1.115318358102467e-14
Out[8]:
1.115318358102467e-14
In [9]:
using Plots
In [10]:
@show nnz(A)
spy(A)

nnz(A) = 4990
Out[10]:
20 40 60 80 100 20 40 60 80 100 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
In [11]:
LxU=Alu.L*Alu.U
@show nnz(LxU)
spy(LxU)

nnz(LxU) = 9468
Out[11]:
20 40 60 80 100 20 40 60 80 100 0 0.01 0.02 0.03 0.04 0.05

This notebook was generated using Literate.jl.