Scientific Computing, TU Berlin, WS 2019/2020, Lecture 04

Jürgen Fuhrmann, WIAS Berlin

Recap¶

Julia type system
Multiple dispatch
Performance issues
Modules

Julia type system¶

Julia is a strongly typed language
Knowledge about the layout of a value in memory is encoded in its type
Prerequisite for performance
There are concrete types and abstract types
See WikiBook for more

Concrete types¶

Every value in Julia has a concrete type
Concrete types correspond to computer representations of objects
Inquire type info using typeof()
One can initialize a variable with an explicitely given fixed type
- Currently posible only in the body of funtions and for return values, not in the global context of Jupyter, REPL

Abstract types¶

Abstract types label concepts which work for a several concrete types without regard to their memory layout etc.
All variables with concrete types corresponding to a given abstract type (must) share a common interface
A common interface consists of a set of methods working for all types exhibiting this interface
The functionality of an abstract type is implicitely characterized by the methods working on it
"duck typing": use the "duck test" — "If it walks like a duck and it quacks like a duck, then it must be a duck" — to determine if an object can be used for a particular purpose

The power of multiple dispatch¶

Multiple dispatch is one of the defining features of Julia
Combined with the the hierarchical type system it allows for powerful generic program design
New datatypes (different kinds of numbers, differently stored arrays/matrices) work with existing code once they implement the same interface as existent ones.
In some respects C++ comes close to it, but for the price of more and less obvious code

Just-in-time compilation and Performance¶

Just-in-time compilation is another feature setting Julia apart
Use the tools from the The LLVM Compiler Infrastructure Project to organize on-the-fly compilation of Julia code to machine code
Tradeoff: startup time for code execution in interactive situations
Multiple steps: Parse the code, analyze data types etc.
Intermediate results can be inspected using a number of macros

Performance¶

Macros for performance testing:

@elapsed: wall clock time used
@allocated: number of allocations
@time: @elapsed and @allocated together
@benchmark: Benchmarking small pieces of code

Julia performace gotchas:¶

Variables changing types
- Type change assumed to be always possible in global context (outside of a function)
- Type change due to inconsequential programming
Memory allocations for intermediate results
See # 7 Julia Gotchas to handle

Structuring your code: modules, files and packages¶

Complex code is split up into several files
Avoid name clashes for code from different places
Organize the way to use third party code

Finding modules in the file system¶

Put single file modules having the same name as the module into a directory which in on the LOAD_PATH
Call "using" or "import" with the module
You can modify your LOAD_PATH by adding e.g. the actual directory

Packages in the file system¶

Packages are found via the same mechanism
Part of the load path are the directory with downloaded packages and the directory with packages under development
Each package is a directory named Package with a subdirectory src
The file Package/src/Package.jl defines a module named Package
More structures in a package:
- Documentation build recipes
- Test code
- Dependency description
- UUID (Universal unique identifier)
Default packages (e.g. the package manager Pkg) are always available
Use the package manager to checkout a new package via the registry

Julia Workflows¶

REPL
Atom/Juno

Developing code with the Julia REPL¶

"using" a package involves compilation delay on startup of session
Best way: never leave Julia session
E.g. edit your code in the editor
Write code, include, run,
- repeat

Revise.jl¶

Adds a command includet which triggers automatic recompile of the included file and those used therein upon change on the disk.
Put this into your ~/.julia/config/startup.jl:

if isinteractive()
    try
        @eval using Revise
        Revise.async_steal_repl_backend()
    catch err
        @warn "Could not load Revise."
    end
end

Start Julia at the command prompt with julia -i

Atom/Juno¶

Calling code from other languages¶

C
python
C++, R $\dots$

ccall¶

C language code has a well defined binary interface
- int $\leftrightarrow\quad$ Int32
- float $\leftrightarrow\quad$ Float32
- double $\leftrightarrow\quad$ Float64
- C arrays as pointers

Create file cadd.c:

open("cadd.c", "w") do io
    write(io, """double cadd(double x, double y) { return x+y; }""")
end

47

Create shared object (a.k.a. "dll") cadd.so
- note the Julia command syntax using backtics

run(`gcc --shared  cadd.c -o libcadd.so`)

Process(`gcc --shared cadd.c -o libcadd.so`, ProcessExited(0))

Define wrapper function cadd using the Julia ccall method
- (:cadd, "libcadd"): call cadd from libcadd.so
- First Float64: return type
- Tuple (Float64,Float64,): parameter types
- x,y: actual data passed
At its first call it will load libcadd.so into Julia
Direct call of compiled C function cadd(), no intermediate wrapper code

cadd(x,y)=ccall((:cadd, "libcadd"), Float64, (Float64,Float64,),x,y)

cadd (generic function with 1 method)

Call wrapper

@show cadd(1.5,2.5);

cadd(1.5, 2.5) = 4.0

Julia uses this method to access a number of higly optimized linear algebra and other libraries

PyCall¶

Both Julia and Python are homoiconic language, featuring reflection
They can parse the elemnts of their own data structures
Possibility to automatically build proxies for python objects in Julia

Define Python function

open("pyadd.py", "w") do io
    write(io, """
def pyadd(x,y):
    return x+y
""")
end

31

Add PyCall package

using Pkg
Pkg.add("PyCall")

  Updating registry at `~/.julia/registries/General`
  Updating git-repo `https://github.com/JuliaRegistries/General.git`
 Resolving package versions...
  Updating `~/.julia/environments/v1.2/Project.toml`
 [no changes]
  Updating `~/.julia/environments/v1.2/Manifest.toml`
 [no changes]

Use PyCall package

using PyCall

Import python module:

pyadd=pyimport("pyadd")

PyObject <module 'pyadd' from '/home/fuhrmann/Wias/teach/scicomp/course/pyadd.py'>

Call pyadd from imported module

@show pyadd.pyadd(3.5,6.5)

pyadd.pyadd(3.5, 6.5) = 10.0

10.0

Julia allows to call almost any python package
E.g. matplotlib graphics
There is also a pyjulia package allowing to call Julia from python

Number representation¶

Numbers of course are represented by bits

@show bitstring(Int16(1))
@show bitstring(Float16(1))
@show bitstring(Int64(1))
@show bitstring(Float64(1))

bitstring(Int16(1)) = "0000000000000001"
bitstring(Float16(1)) = "0011110000000000"
bitstring(Int64(1)) = "0000000000000000000000000000000000000000000000000000000000000001"
bitstring(Float64(1)) = "0011111111110000000000000000000000000000000000000000000000000000"

"0011111111110000000000000000000000000000000000000000000000000000"

Representation of real numbers¶

Any real number $x\in \mathbb{R}$ can be expressed via representation formula: \begin{align*}
```
 x=\pm \sum_{i=0}^{\infty} d_i\beta^{-i} \beta^e
```
\end{align*}
- $\beta\in \mathbb N, \beta\geq 2$: base
- $d_i \in \mathbb N, 0\leq d_i < \beta$: mantissa digits
- $e\in \mathbb Z$ : exponent
Infinite for periodic decimal numbers, irrational numbers

Scientific notation of floating point numbers: e.g.¶

Let $x= 6.022\cdot 10^{23}$
- $\beta=10$
- $d=(6,0,2,2,0\dots)$
- $e=23$
Non-unique: e.g. $x_1= 0.6022\cdot 10^{24}=x$
- $\beta=10$
- $d=(0,6,0,2,2,0\dots)$
- $e=24$

Computer representation of floating point numbers¶

Computer representation uses $\beta=2$, therefore $d_i\in \{0,1\}$
Truncation to fixed finite size: \begin{align*} x=\pm \sum_{i=0}^{t-1} d_i\beta^{-i} \beta^e \end{align*}
$t$: mantissa length
Normalization: assume $d_0=1$ $\Rightarrow$ save one bit for mantissa
- normalization step after operations: adjust mantissa and exponent
$k$: exponent size $-\beta^k+1=L\leq e \leq U = \beta^k-1$
Extra bit for sign
$\Rightarrow$ storage size: $ (t-1) + k + 1$

IEEE 754 floating point types¶

Standardized for many languages
Hardware support usually for 64bit and 32bit

precision	Julia	C/C++	k	t	bits
quadruple	n/a	long double	16	111	128
double	Float64	double	11	53	64
single	Float32	float	8	23	32
half	Float16	n/a	5	10	16

See also the Julia Documentation on floating point numbers

Storage layout for a normalized Float32 number ($d_0=1$)¶

bit 0: sign, $0\to +,\quad 1\to-$
bit $1\dots 8$: $r=8$ exponent bits
- the value $e+2^{r-1}-1=127$ is stored $\Rightarrow$ no need for sign bit in exponent
bit $9\dots 31$: $t=23$ mantissa bits $d_1\dots d_{23}$
$d_0=1$ not stored $\equiv$ "hidden bit"

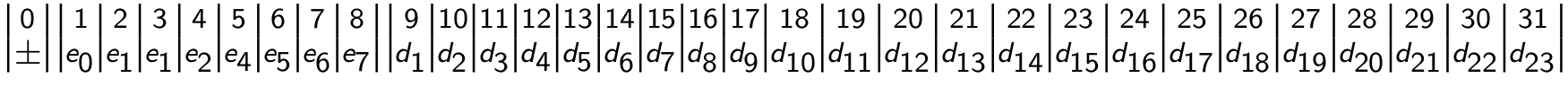
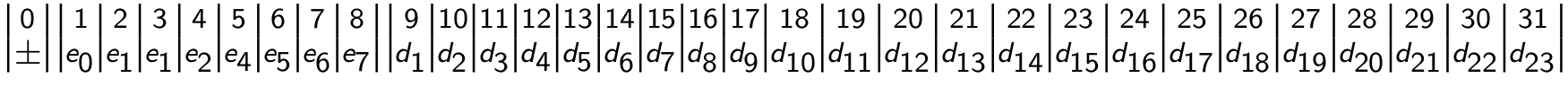
function floatbits(x::Float32)
    s=bitstring(x)
    return s[1]*" "*s[2:9]*" "*s[10:end]
end
function floatbits(x::Float64)
    s=bitstring(x)
    return s[1]*" "*s[2:12]*" "*s[13:end]
end

floatbits (generic function with 2 methods)

$e=0$, stored $e=127$:

floatbits(Float32(1))

"0 01111111 00000000000000000000000"

$e=1$, stored $e=128$:

floatbits(Float32(2))

"0 10000000 00000000000000000000000"

$e=-1$, stored $e=126$:

floatbits(Float32(1/2))

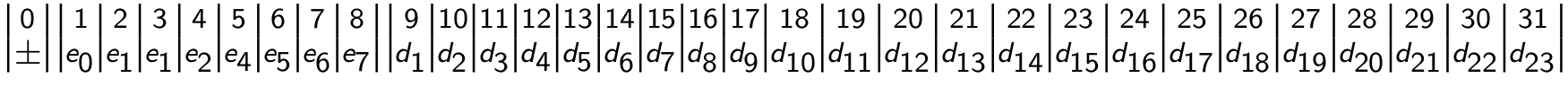
"0 01111110 00000000000000000000000"

Numbers which are exactly represented in decimal system may not be exactly represented in binary system!
Example: infinite periodic number in binary system:

floatbits(Float32(0.1))

"0 01111011 10011001100110011001101"

positive zero:

floatbits(zero(Float32))

"0 00000000 00000000000000000000000"

negative zero:

floatbits(-zero(Float32))

"1 00000000 00000000000000000000000"

Floating point limits¶

Finite size of representation $\Rightarrow$ there are minimal and maximal possible numbers which can be represented
symmetry wrt. 0 because of sign bit
smallest positive denormalized number: $d_i=0, i=0\dots t-2, d_{t-1}=1$ $\Rightarrow$ $x_{min} = \beta^{1-t}\beta^L$

@show nextfloat(zero(Float32));
@show floatbits(nextfloat(zero(Float32)));

nextfloat(zero(Float32)) = 1.0f-45
floatbits(nextfloat(zero(Float32))) = "0 00000000 00000000000000000000001"

@show nextfloat(zero(Float64));
@show floatbits(nextfloat(zero(Float64)));

nextfloat(zero(Float64)) = 5.0e-324
floatbits(nextfloat(zero(Float64))) = "0 00000000000 0000000000000000000000000000000000000000000000000001"

smallest positive normalized number: $d_0=1, d_i=0, i=1\dots t-1$ $\Rightarrow$ $x_{min} = \beta^L$

@show floatmin(Float32);
@show floatbits(floatmin(Float32));

floatmin(Float32) = 1.1754944f-38
floatbits(floatmin(Float32)) = "0 00000001 00000000000000000000000"

@show floatmin(Float64);
@show floatbits(floatmin(Float64));

floatmin(Float64) = 2.2250738585072014e-308
floatbits(floatmin(Float64)) = "0 00000000001 0000000000000000000000000000000000000000000000000000"

largest positive normalized number: $d_i=\beta-1, 0\dots t-1$ $\Rightarrow$ $x_{max} = \beta (1-\beta^{1-t}) \beta^U$

@show floatmax(Float32)
@show floatbits(floatmax(Float32));

floatmax(Float32) = 3.4028235f38
floatbits(floatmax(Float32)) = "0 11111110 11111111111111111111111"

@show floatmax(Float64)
@show floatbits(floatmax(Float64));

floatmax(Float64) = 1.7976931348623157e308
floatbits(floatmax(Float64)) = "0 11111111110 1111111111111111111111111111111111111111111111111111"

largest representable number

@show typemax(Float32)
@show floatbits(typemax(Float32))
@show prevfloat(typemax(Float32));

typemax(Float32) = Inf32
floatbits(typemax(Float32)) = "0 11111111 00000000000000000000000"
prevfloat(typemax(Float32)) = 3.4028235f38

@show typemax(Float64)
@show floatbits(typemax(Float64))
@show prevfloat(typemax(Float64));

typemax(Float64) = Inf
floatbits(typemax(Float64)) = "0 11111111111 0000000000000000000000000000000000000000000000000000"
prevfloat(typemax(Float64)) = 1.7976931348623157e308

Machine precision¶

There cannot be more than $2^{t+k}$ floating point numbers $\Rightarrow$ almost all real numbers have to be approximated
Let $x$ be an exact value and $\tilde x$ be its approximation. Then $|\frac{\tilde x-x}{x}|<\epsilon$ is the best accuracy estimate we can get, where
- $\epsilon=\beta^{1-t}$ (truncation)
- $\epsilon=\frac12\beta^{1-t}$ (rounding)
Also: $\epsilon$ is the smallest representable number such that $1+\epsilon >1$.
Relative errors show up in particular when
- subtracting two close numbers
- adding smaller numbers to larger ones

How do operations work?¶

E.g. Addition

Adjust exponent of number to be added:
- Until both exponents are equal, add one to exponent, shift mantissa to right bit by bit
Add both numbers
Normalize result

The smallest number one can add to 1 can have at most $t$ bit shifts of normalized mantissa until mantissa becomes 0, so its value must be $2^{-t}$.

Machine epsilon¶

Smallest floating point number $\epsilon$ such that $1+\epsilon>1$ in floating point arithmetic
In exact math it is true that from $1+\varepsilon=1$ it follows that $0+\varepsilon=0$ and vice versa. In floating point computations this is not true

ϵ=eps(Float32)
@show ϵ, floatbits(ϵ)
@show one(Float32)+ϵ/2
@show one(Float32)+ϵ,floatbits(one(Float32)+ϵ)
@show nextfloat(one(Float32))-one(Float32);

(ϵ, floatbits(ϵ)) = (1.1920929f-7, "0 01101000 00000000000000000000000")
one(Float32) + ϵ / 2 = 1.0f0
(one(Float32) + ϵ, floatbits(one(Float32) + ϵ)) = (1.0000001f0, "0 01111111 00000000000000000000001")
nextfloat(one(Float32)) - one(Float32) = 1.1920929f-7

ϵ=eps(Float64)
@show ϵ, floatbits(ϵ)
@show one(Float64)+ϵ/2
@show one(Float64)+ϵ,floatbits(one(Float64)+ϵ)
@show nextfloat(one(Float64))-one(Float64);

(ϵ, floatbits(ϵ)) = (2.220446049250313e-16, "0 01111001011 0000000000000000000000000000000000000000000000000000")
one(Float64) + ϵ / 2 = 1.0
(one(Float64) + ϵ, floatbits(one(Float64) + ϵ)) = (1.0000000000000002, "0 01111111111 0000000000000000000000000000000000000000000000000001")
nextfloat(one(Float64)) - one(Float64) = 2.220446049250313e-16

Associativity ?¶

Normally: $(a+b)+c = a+ (b+c)$
But without optimization:

@show (1.0 + 0.5*eps(Float64)) - 1.0
@show 1.0 + (0.5*eps(Float64) - 1.0);

(1.0 + 0.5 * eps(Float64)) - 1.0 = 0.0
1.0 + (0.5 * eps(Float64) - 1.0) = 1.1102230246251565e-16

With optimization:

ϵ=eps(Float64)
@show (1.0 + ϵ/2) - 1.0
@show 1.0 + (ϵ/2 - 1.0);

(1.0 + ϵ / 2) - 1.0 = 0.0
1.0 + (ϵ / 2 - 1.0) = 1.1102230246251565e-16

Density of floating point numbers¶

function fpdens(x::AbstractFloat;sample_size=1000)
    xleft=x
    xright=x
    for i=1:sample_size
        xleft=prevfloat(xleft)
        xright=nextfloat(xright)
    end
    return prevfloat(2.0*sample_size/(xright-xleft))
end

fpdens (generic function with 1 method)

x=10.0 .^collect(-10.0:0.1:10.0)

201-element Array{Float64,1}:
 1.0e-10               
 1.2589254117941662e-10
 1.584893192461111e-10 
 1.9952623149688828e-10
 2.511886431509582e-10 
 3.1622776601683795e-10
 3.9810717055349694e-10
 5.011872336272714e-10 
 6.309573444801942e-10 
 7.943282347242822e-10 
 1.0e-9                
 1.2589254117941663e-9 
 1.584893192461111e-9  
 ⋮                     
 7.943282347242821e8   
 1.0e9                 
 1.258925411794166e9   
 1.5848931924611108e9  
 1.9952623149688828e9  
 2.511886431509582e9   
 3.1622776601683793e9  
 3.9810717055349693e9  
 5.011872336272715e9   
 6.309573444801943e9   
 7.943282347242822e9   
 1.0e10

using Plots
using Plots
plot(x,fpdens.(x), xaxis=:log, yaxis=:log, label="",xlabel="x", ylabel="floating point numbers per unit interval")

Matrix + Vector norms¶

Vector norms: let $x= (x_i)\in \mathbb R^n$¶

using LinearAlgebra
x=[3.0,2.0,5.0]

3-element Array{Float64,1}:
 3.0
 2.0
 5.0

$||x||_1 = \sum_{i=1}^n |x_i|$: sum norm, $l_1$-norm

@show norm(x,1);

norm(x, 1) = 10.0

$||x||_2 = \sqrt{\sum_{i=1}^n x_i^2}$: Euclidean norm, $l_2$-norm

@show norm(x,2);
@show norm(x);

norm(x, 2) = 6.164414002968976
norm(x) = 6.164414002968976

$||x||_\infty = \max_{i=1}^n |x_i|$: maximum norm, $l_\infty$-norm

@show norm(x, Inf);

norm(x, Inf) = 5.0

Matrix $A= (a_{ij})\in \mathbb R^{n} \times \mathbb R^{n}$

Representation of linear operator $\mathcal A: \mathbb R^{n} \to \mathbb R^{n}$ defined by $\mathcal A: x\mapsto y=Ax$ with \begin{align*}
```
 y_i= \sum_{j=1}^n a_{ij} x_j
```
\end{align*}

Induced matrix norm: \begin{align*}

 ||A||_p&=\max_{x\in \mathbb R^n,x\neq 0} \frac{||Ax||_p}{||x||_p}\\
 &=\max_{x\in \mathbb R^n,||x||_p=1} \frac{||Ax||_p}{||x||_p}

\end{align*}

Matrix norms induced from vector norms¶

A=[3.0 2.0 5.0; 0.1  0.3  0.5 ; 0.6  2 3]

3×3 Array{Float64,2}:
 3.0  2.0  5.0
 0.1  0.3  0.5
 0.6  2.0  3.0

$||A||_1= \max_{j=1}^n \sum_{i=1}^n |a_{ij}|$ maximum of column sums of absolute values of entries

@show opnorm(A,1);

opnorm(A, 1) = 8.5

$||A||_\infty= \max_{i=1}^n \sum_{j=1}^n |a_{ij}|$ maximum of row sums of absolute values of entries

@show opnorm(A,Inf);

opnorm(A, Inf) = 10.0

$||A||_2=\sqrt{\lambda_{max}}$ with $\lambda_{max}$: largest eigenvalue of $A^TA$.

@show opnorm(A,2);

opnorm(A, 2) = 7.083763693021976

Matrix condition number and error propagation¶

Problem: solve $Ax=b$, where $b$ is inexact
Let $\Delta b$ be the error in $b$ and $\Delta x$ be the resulting error in $x$ such that \begin{equation*} A(x+\Delta x)=b+\Delta b. \end{equation*}
Since $Ax=b$, we get $A\Delta x=\Delta b$
Therefore \begin{equation*} \left { \begin{array}{rl}
```
 \Delta x&=A^{-1} \Delta b\\ Ax&=b
```
\end{array} \right} \Rightarrow \left{ \begin{array}{rl}
```
 ||A||\cdot ||x||&\geq||b|| \\ ||\Delta x||&\leq ||A^{-1}||\cdot ||\Delta b||
\end{array} \right.
```
\end{equation*}

\begin{equation*} \Rightarrow \frac{||\Delta x||}{||x||} \leq \kappa(A) \frac{||\Delta b||}{||b||} \end{equation*}

where $\kappa(A)= ||A||\cdot ||A^{-1}||$ is the condition number of $A$.

Error propagation:¶

A=[ 1.0 -1.0 ; 1.0e5 1.0e5];
Ainv=inv(A)
κ=opnorm(A)*opnorm(Ainv)
@show Ainv
@show κ;

Ainv = [0.5 5.0e-6; -0.5 5.0e-6]
κ = 100000.0

x=[ 1.0, 1.0]
b=A*x
@show b
Δb=1*[eps(1.0), eps(1.0)]
Δx=Ainv*(b+Δb)-x
@show norm(Δx)/norm(x)
@show norm(Δb)/norm(b)
@show κ*norm(Δb)/norm(b)

b = [0.0, 200000.0]
norm(Δx) / norm(x) = 7.850462293418875e-17
norm(Δb) / norm(b) = 1.5700924586837751e-21
(κ * norm(Δb)) / norm(b) = 1.5700924586837752e-16

1.5700924586837752e-16

This notebook was generated using Literate.jl.