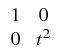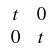Collaborator: J. Elschner (FG 4),
H.-Chr. Kaiser (FG 1),
J. Rehberg (FG 1),
G. Schmidt
(FG 4)
Description:
The reported work continues efforts to prove existence, uniqueness, and
regularity results for elliptic and parabolic equations and systems
which describe phenomena in physics, chemistry, and biology (see Annual
Research Reports 2000, p. 19 et sqq., 2002, p. 39 et sqq., and 2003,
p. 178 et sqq.).
In view of the applications which we have in mind, one is nearly
always confronted with nonsmooth domains, discontinuous coefficients
and/or mixed boundary conditions. In particular, in simulation of the
current flow in real semiconductor devices---a project area of
WIAS---the latter is unavoidable, or the model is meaningless,
[18]. As is well known, the usual regularity properties which
hold in case of smooth constellations then break down. So, one has to
look for suitable substitutes. It turns out that for the successful
treatment of such equations it is of great use to have optimal
regularity results for the corresponding elliptic operators
-  .
. 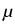
 between
W1, q
between
W1, q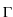 and
W-1, q
and
W-1, q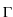 (with homogeneous Dirichlet boundary conditions on
(with homogeneous Dirichlet boundary conditions on
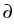

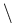
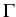 ) at hand where q is larger than the
space dimension. In [12], Gröger proved that q may be
taken always larger than 2 under very general conditions on the
domain, the coefficients, and the Neumann boundary part. This result
is very useful in many spatially two-dimensional applications, see
[2, 4,
9, 11, 14]. One cannot expect q > 3 in this general
setting (see [17] and the Example below). But the necessity
grows to study not only two-dimensional problems (mostly as cuts of
the original three-dimensional ones) but the three-dimensional
models themselves; this means that one needs q > 3. This is true in
semiconductor device modeling (see [10],
[15]) but also in many other application areas. Thus, we
intend to define a class of three-dimensional domains
) at hand where q is larger than the
space dimension. In [12], Gröger proved that q may be
taken always larger than 2 under very general conditions on the
domain, the coefficients, and the Neumann boundary part. This result
is very useful in many spatially two-dimensional applications, see
[2, 4,
9, 11, 14]. One cannot expect q > 3 in this general
setting (see [17] and the Example below). But the necessity
grows to study not only two-dimensional problems (mostly as cuts of
the original three-dimensional ones) but the three-dimensional
models themselves; this means that one needs q > 3. This is true in
semiconductor device modeling (see [10],
[15]) but also in many other application areas. Thus, we
intend to define a class of three-dimensional domains  ,
(possibly discontinuous) coefficient functions
,
(possibly discontinuous) coefficient functions 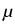 , and Neumann
boundary parts
, and Neumann
boundary parts 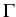 such that
such that
is a topological isomorphism for a q > 3 (and, hence, by interpolation
and duality, for all
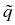
 [q', q]). Let us emphasize that our
principal aim is to generate a setting where many situations of
practical relevance, subject to research at the Weierstrass Institute
and elsewhere, are included.
[q', q]). Let us emphasize that our
principal aim is to generate a setting where many situations of
practical relevance, subject to research at the Weierstrass Institute
and elsewhere, are included.
For some nonsmooth situations one has this already at hand: the pure
Dirichlet and Neumann Laplacian on Lipschitz domains was considered in
[13] and [19], respectively. Concerning
mixed boundary conditions, M. Dauge proved in [3] the
following result:
Proposition 1. Let  be a convex polyhedron and
be a convex polyhedron and 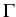 be the Neumann boundary part of
be the Neumann boundary part of
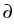
 . If
. If
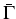
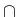 (
(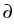

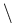
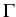 ) is a connected curve which
consists of finitely many line segments, then
is a topological isomorphism for some q > 3.
) is a connected curve which
consists of finitely many line segments, then
is a topological isomorphism for some q > 3.
Let us emphasize that in particular the suppositions are fulfilled if
 is the unit cube and
is the unit cube and 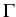 is one half of its ground
plate.
is one half of its ground
plate.
While in the afore-mentioned cases, the coefficients are constant, we
proved in a joint paper [16] with V. Maz'ya the
following result:
Theorem 1. Let  be a Lipschitzian polyhedron which
splits up into finitely many subpolyhedra. Let
be a Lipschitzian polyhedron which
splits up into finitely many subpolyhedra. Let 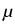 be a coefficient
function on
be a coefficient
function on  which takes its values in the set of real,
symmetric, positive definite 3 x 3 matrices and is constant on
any subpolyhedron.
which takes its values in the set of real,
symmetric, positive definite 3 x 3 matrices and is constant on
any subpolyhedron.
For any edge E and
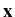
 E take an orthogonal transformation
E take an orthogonal transformation
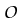 E which transforms this edge into a line which is parallel
to the z-axis. Consider the resulting transformed coefficient matrix
function
E which transforms this edge into a line which is parallel
to the z-axis. Consider the resulting transformed coefficient matrix
function
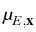 under the mapping
under the mapping
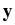
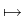
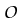 E
E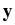 -
- 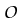 E
E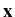 . Denote by
. Denote by 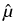 the upper left
2 x 2
matrix function, restricted to the intersection of the x-y plane
with
the upper left
2 x 2
matrix function, restricted to the intersection of the x-y plane
with
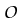 E(
E( -
- 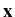 ). By passing to
polar coordinates
(r,
). By passing to
polar coordinates
(r,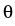 ), multiplying by r2, and taking the
Mellin transform with respect to r, one obtains from the
corresponding two-dimensional boundary value problem the following
one-dimensional problem with parameter
), multiplying by r2, and taking the
Mellin transform with respect to r, one obtains from the
corresponding two-dimensional boundary value problem the following
one-dimensional problem with parameter 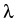 on an interval of
angles
on an interval of
angles
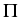 ( (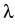 ) )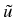  - - 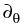 (b2 (b2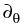 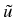 ) - ) - 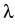 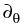 (b1 (b1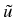 ) - ) - 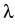 b1 b1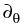 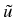 - - 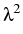 b0 b0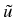 = = 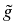 , ,
|
(3) |
supplemented by transmission conditions (see [16]
for details).
If for every edge E, the possible 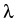 s, satisfying
(3) with right-hand side zero and the transmission
conditions, have real parts not contained in the interval ]0, 1/3],
then there is a q > 3 such that
s, satisfying
(3) with right-hand side zero and the transmission
conditions, have real parts not contained in the interval ]0, 1/3],
then there is a q > 3 such that
is a topological isomorphism.
Unfortunately, for each edge the set of occurring 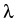 s is
identical with the set of zeros of a transcendental equation which is
not at all easy to discuss in general. Nevertheless, we succeeded in
proving the following result which covers completely the case of
polygonal, layered structures:
s is
identical with the set of zeros of a transcendental equation which is
not at all easy to discuss in general. Nevertheless, we succeeded in
proving the following result which covers completely the case of
polygonal, layered structures:
Theorem 2 (to be published in [7]). Assume that the
following conditions are fulfilled:  is a three-dimensional
Lipschitzian polyhedron. There are hyperplanes
is a three-dimensional
Lipschitzian polyhedron. There are hyperplanes
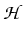 1...
1...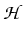 n in R3 intersecting (within
n in R3 intersecting (within
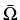 ) with
each other at most in a vertex of the polyhedron such that the
coefficient function
) with
each other at most in a vertex of the polyhedron such that the
coefficient function 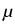 is a constant real symmetric positive
definite
3 x 3 matrix on each of the connected components of
is a constant real symmetric positive
definite
3 x 3 matrix on each of the connected components of

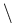
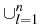
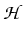 l. Moreover, for every
edge on the boundary, induced by a hetero-interface
l. Moreover, for every
edge on the boundary, induced by a hetero-interface
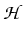 l,
the angles between the outer boundary plane and the hetero-interface
do not exceed
l,
the angles between the outer boundary plane and the hetero-interface
do not exceed 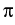 and at most one of them may equal
and at most one of them may equal 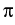 . Then
the operator
-
. Then
the operator
-  .
. 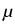
 provides a topological
isomorphism between
W01, q(
provides a topological
isomorphism between
W01, q( ) and
W-1, q(
) and
W-1, q( ) for
all
q
) for
all
q  [2, 4].
[2, 4].
In the case of nonsmooth interfaces, q exceeds 2 only arbitrarily
little, as the following instructive counterexample by J. Elschner
shows.
Example (to be published in [7]).
Consider the following coefficient function 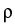 on R2:
on R2:
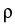
(
x,
y) =
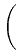
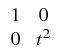
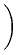
if
x,
y > 0 and
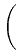
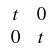
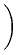
elsewhere on
R2
(t positive) and, correspondingly, the following elliptic problem on
R2:
 . . 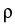  w = 0, w w = 0, w 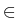 W1, 2loc(R2). W1, 2loc(R2).
|
(4) |
Following again [16], one evaluates the 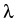 s
with the smallest positive real part as
If
t
s
with the smallest positive real part as
If
t 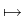
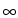 , then the real part of
, then the real part of 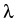 converges to
0. This provides a local solution of (4) which behaves
like
(x2 + y2)
converges to
0. This provides a local solution of (4) which behaves
like
(x2 + y2)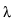 /2 in a neighborhood of 0
/2 in a neighborhood of 0  R2.
Tending with t to
R2.
Tending with t to 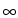 , these solutions lack any common (local)
integrability of order larger than 2 for their first-order
derivatives.
, these solutions lack any common (local)
integrability of order larger than 2 for their first-order
derivatives.
Clearly, the example is not restricted to two dimensions, namely, one
can add arbitrarily many dimensions by extending the solution
constantly in these directions---at least in a neighborhood of zero.
However, in case of an inner C1 interface, we proved the following
result which generalizes the linear regularity result of [1].
Theorem 3 (to be published in [8]). Let  be a Lipschitz domain and
be a Lipschitz domain and
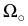
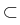
 be a C1
domain which does not touch the boundary of
be a C1
domain which does not touch the boundary of  . Suppose that the
coefficient function
. Suppose that the
coefficient function 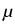 is uniformly continuous on
is uniformly continuous on

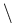
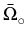 and on
and on
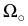 . Then there is a
q > 3 such that
is a topological isomorphism.
. Then there is a
q > 3 such that
is a topological isomorphism.
Further, from Proposition 1 one may conclude by localization
techniques and perturbation arguments the following
Theorem 4 (to be published in [8]). Let
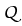
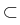 R3 denote the unit cube and
R3 denote the unit cube and 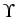 one half of its
ground plate. Assume that the coefficient function
one half of its
ground plate. Assume that the coefficient function 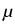 is uniformly
continuous. For any
is uniformly
continuous. For any
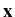

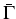
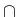 (
(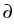

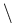
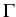 ) there is an open neighborhood
) there is an open neighborhood
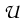
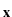 in R3 and a homeomorphism
in R3 and a homeomorphism
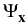 from
from
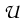
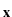 onto an open set
onto an open set
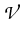
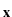 which satisfy
which satisfy
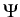 (
(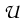
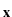
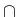 (
(
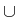
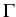 ) =
) = 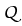
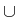
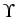 and
and
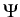 (
(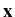 ) = 0. Moreover, every
) = 0. Moreover, every
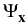 and its inverse are
continuously differentiable and the derivative is uniformly continuous
on
and its inverse are
continuously differentiable and the derivative is uniformly continuous
on
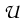
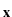 .
Then there is a q > 3 such that
-
.
Then there is a q > 3 such that
-  .
. 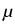
 is a
topological isomorphism between
W1, q
is a
topological isomorphism between
W1, q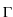 and
W-1, q
and
W-1, q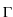 .
.
Finally, one can define a global setting which includes all the above-mentioned
situations in a certain sense as its local constituents, see
[8].
References:
- L.A. CAFFARELLI, I. PERAL, On W1, p
estimates for elliptic equations in divergence form, Comm. Pure
Appl. Math., 51 (1998), pp. 1-21.
- L. CONSIGLIERI, M.M.C.
MUNIZ, Existence of solutions for a free boundary problem in
the thermoelectrical modelling of an aluminium electrolytic cell,
Eur. J. Appl. Math., 14 (2003), pp. 201-216.
- M. DAUGE, Neumann and mixed problems
on curvilinear polyhedra, Integral Equations Operator Theory,
15 (1992), pp. 227-261.
- P. DEGOND, S.
GÉNIEYS, A. JÜNGEL, A
steady-state system in non-equilibrium thermodynamics including
thermal and electrical effects, Math. Methods Appl. Sci.,
21 (1998), pp. 1399-1413.
- J. ELSCHNER, G. SCHMIDT,
Diffraction in periodic structures and optimal design of binary
gratings. I. Direct problems and gradient formulas, Math. Methods Appl.
Sci., 21 (1998), pp. 1297-1342.
- J. ELSCHNER, R. HINDER,
F. PENZEL, G. SCHMIDT,
Existence, uniqueness and regularity for solutions of the conical
diffraction problem, Math. Models Methods Appl. Sci.,
10 (2000), pp. 317-341,
- J. ELSCHNER, H.-CHR.
KAISER, J. REHBERG, G.
SCHMIDT, W1, q regularity results for elliptic
transmission problems on heterogeneous polyhedra, in preparation.
-
, Optimal regularity for elliptic
operators occurring in real-world problems,
in preparation.
- P. FABRIE, T. GALLOU╦T, Modeling wells in porous media flow, Math. Models Methods
Appl. Sci., 10 (2000), pp. 673-709.
- H. GAJEWSKI, H.-CHR.
KAISER, H. LANGMACH, R.
NÜRNBERG, R.H. RICHTER, Mathematical modeling and numerical simulation of semiconductor
detectors, in: Mathematics--Key Technology for the Future. Joint
Projects Between Universities and Industry, W. Jäger,
H.J. Krebs, eds., Springer-Verlag, Berlin, Heidelberg, 2003,
pp. 355-364.
- A. GLITZKY, R.
HÜNLICH, Global estimates and asymptotics for
electro-reaction-diffusion systems in heterostructures,
Appl. Anal., 66 (1997), pp. 205-226.
- K. GRÖGER, A W1, p-estimate
for solutions to mixed boundary value problems for second order
elliptic differential equations, Math. Ann., 283 (1989),
pp. 679-687.
- D. JERISON, C.E. KENIG,
The inhomogeneous Dirichlet problem in Lipschitz domains,
J. Funct. Anal., 130 (1995), pp. 161-219.
- A. JÜNGEL, Regularity and
uniqueness of solutions to a parabolic system in nonequilibrium
thermodynamics, Nonlinear Anal. TMA, 41
(2000), pp. 669-688.
- G. LUTZ, R.H. RICHTER, L. STRÜDER,
DEPMOS-Arrays for X-ray imaging, in: XRAY Optics, Instruments and
Missions III, J. Trümper, B. Aschenbach, eds., Proceedings of
SPIE, 4012 (2000), pp. 249-256.
- V. MAZ'YA, J.
ELSCHNER, J. REHBERG, G.
SCHMIDT, Solutions for quasilinear nonsmooth evolution
systems in Lp, Arch. Ration. Mech. Anal., 171 (2004),
pp. 219-262.
- N.G. Meyers, An Lp-estimate for the gradient of
solutions of second order elliptic divergence equations, Ann.
Scuola Norm. Sup. Pisa Cl. Sci., 17 (1963), pp. 189-206.
- S. SELBERHERR, Analysis and simulation of
semiconductor devices, Springer-Verlag, Wien, New York, 1984.
- D. ZANGER, The inhomogeneous Neumann
problem in Lipschitz domains, Comm. Partial Differential Equations,
25 (2000), pp. 1771-1808.
LaTeX typesetting by H. Pletat
2005-07-29
![]() .
. ![]()
![]() between
W1, q
between
W1, q![]() and
W-1, q
and
W-1, q![]() (with homogeneous Dirichlet boundary conditions on
(with homogeneous Dirichlet boundary conditions on
![]()
![]()
![]()
![]() ) at hand where q is larger than the
space dimension. In [12], Gröger proved that q may be
taken always larger than 2 under very general conditions on the
domain, the coefficients, and the Neumann boundary part. This result
is very useful in many spatially two-dimensional applications, see
[2, 4,
9, 11, 14]. One cannot expect q > 3 in this general
setting (see [17] and the Example below). But the necessity
grows to study not only two-dimensional problems (mostly as cuts of
the original three-dimensional ones) but the three-dimensional
models themselves; this means that one needs q > 3. This is true in
semiconductor device modeling (see [10],
[15]) but also in many other application areas. Thus, we
intend to define a class of three-dimensional domains
) at hand where q is larger than the
space dimension. In [12], Gröger proved that q may be
taken always larger than 2 under very general conditions on the
domain, the coefficients, and the Neumann boundary part. This result
is very useful in many spatially two-dimensional applications, see
[2, 4,
9, 11, 14]. One cannot expect q > 3 in this general
setting (see [17] and the Example below). But the necessity
grows to study not only two-dimensional problems (mostly as cuts of
the original three-dimensional ones) but the three-dimensional
models themselves; this means that one needs q > 3. This is true in
semiconductor device modeling (see [10],
[15]) but also in many other application areas. Thus, we
intend to define a class of three-dimensional domains ![]() ,
(possibly discontinuous) coefficient functions
,
(possibly discontinuous) coefficient functions ![]() , and Neumann
boundary parts
, and Neumann
boundary parts ![]() such that
such that
![]() is the unit cube and
is the unit cube and ![]() is one half of its ground
plate.
is one half of its ground
plate.
![]()
![]() E take an orthogonal transformation
E take an orthogonal transformation
![]() E which transforms this edge into a line which is parallel
to the z-axis. Consider the resulting transformed coefficient matrix
function
E which transforms this edge into a line which is parallel
to the z-axis. Consider the resulting transformed coefficient matrix
function
![]() under the mapping
under the mapping
![]()
![]()
![]() E
E![]() -
- ![]() E
E![]() . Denote by
. Denote by ![]() the upper left
2 x 2
matrix function, restricted to the intersection of the x-y plane
with
the upper left
2 x 2
matrix function, restricted to the intersection of the x-y plane
with
![]() E(
E(![]() -
- ![]() ). By passing to
polar coordinates
(r,
). By passing to
polar coordinates
(r,![]() ), multiplying by r2, and taking the
Mellin transform with respect to r, one obtains from the
corresponding two-dimensional boundary value problem the following
one-dimensional problem with parameter
), multiplying by r2, and taking the
Mellin transform with respect to r, one obtains from the
corresponding two-dimensional boundary value problem the following
one-dimensional problem with parameter ![]() on an interval of
angles
on an interval of
angles
![]() s, satisfying
(3) with right-hand side zero and the transmission
conditions, have real parts not contained in the interval ]0, 1/3],
then there is a q > 3 such that
s, satisfying
(3) with right-hand side zero and the transmission
conditions, have real parts not contained in the interval ]0, 1/3],
then there is a q > 3 such that
![]() s is
identical with the set of zeros of a transcendental equation which is
not at all easy to discuss in general. Nevertheless, we succeeded in
proving the following result which covers completely the case of
polygonal, layered structures:
s is
identical with the set of zeros of a transcendental equation which is
not at all easy to discuss in general. Nevertheless, we succeeded in
proving the following result which covers completely the case of
polygonal, layered structures: