[Next]:

Modeling, analysis and simulation of mode-locked

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index] 

Calculation of electronic band structure of InAsSb multi quantum wells

Collaborator: U. Bandelow (FG 1), M. Baro (FG 1), Th. Koprucki (FG 3)

Cooperation with: J. Tomm and F. Weik (both Max-Born-Institut für Nichtlineare Optik und Kurzzeitspektroskopie (MBI), Berlin), M. Grau (Walter-Schottky-Institut, Technische Universität München)

Supported by: MBI, DFG: Research Center MATHEON, project D4; Priority Program ``Analysis, Modellbildung und Simulation von Mehrskalenproblemen'' (Analysis, Modeling and Simulation of Multiscale Problems)

Description:

Indium-arsenide-antimonide (InAsSb) heterostructures, having the lowest band gap of all III-V semiconductors, are of great interest in the recent development of infrared optoelectronic devices like lasers and photodetectors. The aim of the project is the calculation of the electronic band structure of InAsSb multi-quantum-well (MQW) lasers.

The MQW structures we investigate are grown at the Walter Schottky Institute and are potential candidates for the optically active region of infrared LEDs. The structures consist of a stack of 10 -nm-thick strained InAs_xSb_1-x quantum wells sandwiched between 20  nm or 40  nm Al_0.15In_0.85As_0.78Sb_0.22 barriers. The arsenic content of the well material varies between the samples, which leads to a different strain for each sample. The investigation of the influence of the strain on the bandgap is a central point of the investigations.

Characterization and measurements of the structures are carried out at the Max Born Institute (MBI).

The most economical description of the energy bands in semiconductors is the multiband k ^. p method. According to this method the quantum-confined states F_$\mu$l(z;$\bf k_\Vert$) and the corresponding subband dispersions E_l($\bf k_\Vert$) are solutions of the respective eigenvalue problem

$$\mu \nu \left(\vphantom{{\bf k_\Vert},k_\perp =-i\frac{\partial}{\partial z};\ldots}\right. \bf k_\Vert \perp {\frac{{\partial}}{{\partial z}}} \left.\vphantom{{\bf k_\Vert},k_\perp =-i\frac{\partial}{\partial z};\ldots}\right) \nu \bf k_\Vert \bf k_\Vert \mu \bf k_\Vert$$ (1)

where z denotes the growth direction. For consistently modeling the mixing of conduction and valence bands in our low-gap material we use eight-band k ^. p Hamiltonians H_$\mu$$\nu$. The structure of the corresponding Hamiltonians can be found in [2], their spectral properties are studied in [3]. The WIAS-QW software package (see [1]) uses an eight-band k ^. p model and is successfully applied to the simulation of the InAsSb/AlInAsSb nanostructures described above. Moreover, the results are compared with the measured values of MBI.

Our simulation parameters are obtained from Vurgaftman et al. [4] by means of the ternary and quaternary interpolation schemes described there. The bandgap E_g and the spin-split-off energy are obtained by quadratic interpolation, whereas the remaining material parameters are derived by linear interpolation. For the calculations, the in-plane strain is determined by the formula (a₀ - a)/a, where a₀ = 0.6096 nm is the lattice constant of the GaSb substrate, and a is the lattice constant of the corresponding layer material. The calculated strain values agree with the measured values. The calculated bandgap varies linearly with the strain, with a slope of about 84  meV, which compares well with the experimental findings obtained by MBI, [5].

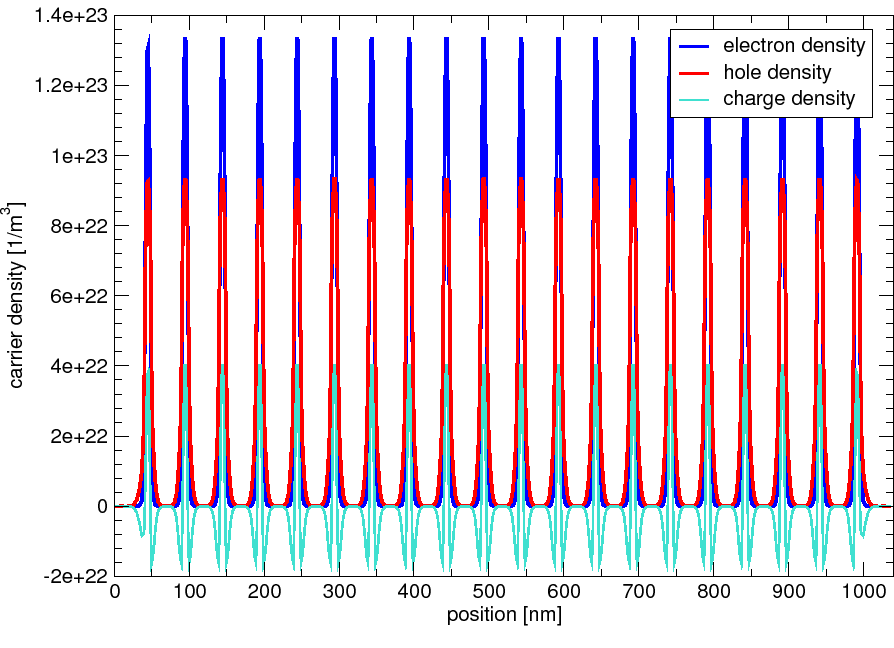
As an example, we plot the subband structure of one sample in Figure 1. It exhibits a strong nonparabolicity, especially for the valence subbands. For the latter, also strong warping (angular dependence) is detected, which is also a result of the band-band interaction, which involves electrons, heavy holes, light holes, and spin-split-off holes.

 

For further illustration, we plot the local density distributions within the MQW structures for our selected sample in Figure 1. For these illustrations, we assume charge neutrality with sheet densities given by N = P = 10¹¹/cm². We observe very good confinement of the electrons as well as of the holes within the quantum wells. That is, their difference (which is the net charge density) remains small and not much screening takes place. As can also be seen by the density distribution in Figure 2, the quantum wells are well isolated from each other by the barriers, such that calculations with single quantum wells yield the same results as calculations on the full MQW structure.

Fig. 2: Local carrier density distribution in the MQW region of a selected sample with 20 quantum wells for a sheet density N = P = 10¹¹/cm². Blue: electron density n, red: hole density p, cyan: charge density n - p.

References:

1. http://www.wias-berlin.de/software/qw/.

2. P. ENDERS, A. BÄRWOLFF, M. WOERNER, D. SUISKY, kp theory of energy bands, wave functions, and optical selection rules in strained tetrahedral semiconductors, Phys. Rev. B, 51(23) (1995), pp. 16695-16704.

3. U. BANDELOW, H.-CHR. KAISER, TH. KOPRUCKI, J. REHBERG, Spectral properties of k ^. p Schrödinger operators in one space dimension, Numer. Funct. Anal. Optim., 21(3&4) (2000), pp. 379-409.

4. I. VURGAFTMAN, J.R. MEYER, L.R. RAM-MOHAN, Band parameters for III/V compound semiconductors and their alloys, J. Appl. Phys., 89 (2001), pp. 5815-5875.

5. TH. KOPRUCKI, M. BARO, U. BANDELOW, T.Q. TIEN, F. WEIK, J.W. TOMM, M. GRAU, M.-CHR. AMANN, Electronic structure and optoelectronic properties of strained InAsSb/GaSb multi quantum-wells, WIAS Preprint no. 1028, 2005 .

[Next]:

Modeling, analysis and simulation of mode-locked

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index]