|
|
|
[Contents] | [Index] |
Collaborator: W. Dreyer, F. Duderstadt
Cooperation with: M. Jurisch, S. Eichler (Freiberger Compound Materials GmbH (FCM)), P. Rudolph, F. Kießling (Institut für Kristallzüchtung, Berlin), K. Haack (GTT-Technologies, Herzogenrath)
Description:
The necessary heat treatment of single crystal semi-insulating gallium arsenide (GaAs), which is deployed in micro- and optoelectronic devices, generates undesirable liquid precipitates in the solid phase. The appearance of precipitates is influenced by surface tension at the liquid/solid interface and deviatoric stresses in the solid. The central quantity for the description of the various aspects of phase transitions is the chemical potential, which can be additively decomposed into a chemical and a mechanical part. In particular, the calculation of the mechanical part of the chemical potential is of crucial importance. We determine the chemical potential in the framework of the St. Venant-Kirchhoff law, which gives an appropriate stress/strain relation for many solids in the small strain regime. We establish criteria which allow the correct replacement of the St. Venant-Kirchhoff law by the simpler Hooke law.
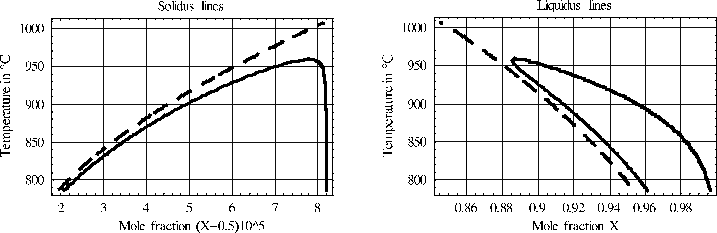
One important application of the model is the calculation of non-standard phase diagrams for GaAs above 786 °C, i.e. those that take into account surface tension and non-deviatoric stresses. The calculation of non-standard phase diagrams relies on the determination of the extrema of the available free energy of the considered thermodynamic system, whereas standard phase diagrams take exclusively the minima into account, [3].
We compare the results with classical phase diagrams where these phenomena are ignored.

We observe that in the temperature range where two phases may coexist, there are two extrema for a given temperature. The parts of the solidus and liquidus lines of the non-standard phase diagram which are located near the solidus and liquidus lines, respectively, of the standard phase diagram consist of minima of the available free energy. The remaining parts of the solidus and liquidus lines correspond to maxima. The minima describe stable droplets, whereas the maxima may be related to critical droplets in the following sense: A droplet that appears by fluctuation with a radius which is smaller than the critical radius will disappear, whereas the droplet will further grow, if it has initially a radius which is larger than the critical radius. A further difference to the standard phase diagram is a dependence of the non-standard phase diagram on the total mole number of the atoms of the system. A doubling increases the range of temperature where both phases may coexist by 5 °K.
The calculation of non-standard phase diagrams is a new subject of thermodynamics, and the results currently meet a growing interest, in particular, in the community of producers of standard phase diagrams. It is planned to transfer the model, which is up to now especially designed to describe precipitation in semi-insulating GaAs, to other materials and processes, like the formation of cementite in steel.
References:
|
|
|
[Contents] | [Index] |