|
|
|
[Contents] | [Index] |
Collaborator: W. Dreyer, F. Duderstadt
Cooperation with: B. Niethammer (Humboldt-Universität zu Berlin), M. Jurisch, S. Eichler (Freiberger Compound Materials GmbH (FCM)), P. Rudolph, F. Kießling (Institut für Kristallzüchtung, Berlin), K. Haack (GTT-Technologies, Herzogenrath)
Description:
The Becker/Döring (BD) model describes processes where a droplet with
![]() atoms may grow by incorporation of a single atom from the surroundings
and shrink by emitting a single atom into the surroundings. Other
processes, like the appearance of a droplet with
atoms may grow by incorporation of a single atom from the surroundings
and shrink by emitting a single atom into the surroundings. Other
processes, like the appearance of a droplet with
![]() +
+ ![]() atoms by the
reaction of a droplet with
atoms by the
reaction of a droplet with ![]() > 1 atoms with another droplet with
> 1 atoms with another droplet with
![]() > 1 atoms, are not considered within the BD model.
> 1 atoms, are not considered within the BD model.
The transition rates of the two processes give the number of reactions per
second, and they are denoted by
![]() and
and
![]() . Their derivation for the case of precipitation of liquid droplets in
GaAs is one of the objectives of this study.
. Their derivation for the case of precipitation of liquid droplets in
GaAs is one of the objectives of this study.
We consider a distribution of droplets with
![]()
![]() {1, 2,...,
{1, 2,...,![]() } atoms
and we introduce a set of functions
Z(t,
} atoms
and we introduce a set of functions
Z(t,![]() )
) ![]() 0, which give at any time
t
0, which give at any time
t ![]() 0 the number of droplets with
0 the number of droplets with ![]() atoms. The number of single
atoms is included here and it is given by Z(t, 1). The choice of the largest
considered droplet with
atoms. The number of single
atoms is included here and it is given by Z(t, 1). The choice of the largest
considered droplet with ![]() atoms is a subtle problem, which is not
discussed here.
atoms is a subtle problem, which is not
discussed here.
The evolution of
Z(t,![]() ) is determined by a system of ordinary
differential equations that we call nowadays the BD system. For a
thermodynamic system with a fixed number of atoms, it reads
) is determined by a system of ordinary
differential equations that we call nowadays the BD system. For a
thermodynamic system with a fixed number of atoms, it reads
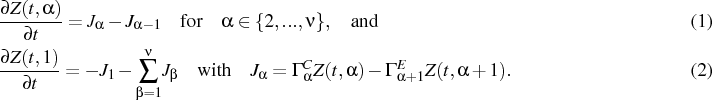
Equilibrium is established for
J![]() = 0, and a thermodynamic treatment
provides the distribution of droplets in equilibrium by minimizing the
available free energy of the system
= 0, and a thermodynamic treatment
provides the distribution of droplets in equilibrium by minimizing the
available free energy of the system
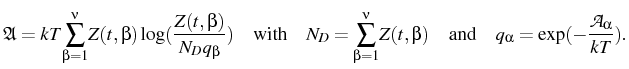
|
(3) |
One of the important results which were obtained during the period of this
report regards the observation that the transition rates
![]() and
and
![]() are not independent from each other because
we have proved the
are not independent from each other because
we have proved the
Theorem:
A sufficient condition that the BD system implies the existence of a
Lyapunov function
that can be identified with
![]() reading
reading
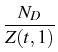 |
(4) |
References:
|
|
|
[Contents] | [Index] |