[Next]:

Optimal control of production processes

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index] 

Optimization and inverse problems in diffractive optics and electromagnetics

Collaborator: J. Elschner, K. Eppler, A. Rathsfeld, G. Schmidt

Cooperation with: G. Bao (Michigan State University, East Lansing, USA), F. Courty (Technische Universität Berlin), A. Erdmann (Frauenhofer-Institut IISB, Erlangen), R. Güther (Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin), H. Harbrecht (Christian-Albrechts-Universität zu Kiel), B. Kleemann (Carl Zeiss AG Oberkochen), R. Schneider (Christian-Albrechts-Universität zu Kiel), M. Yamamoto (University of Tokyo, Japan)

Supported by: Carl Zeiss AG Oberkochen

Description:

1. Efficient simulation and optimization tools for the diffraction by optical gratings (A. Rathsfeld and G. Schmidt).

If the periodic cross-section structure of an optical grating is determined by one or two simple profile curves, then the best method of computation for the electromagnetic field is likely to be the integral equation method. The program package IESMP (cf. [16]) of our cooperation partner Carl Zeiss Oberkochen realizes the boundary element field simulation and the subsequent determination of efficiencies and phase shifts corresponding to the reflected and transmitted modes. Last year we have started to extend the package by a spline collocation method adapted to corner profiles and thin coated layers, and this year we have finished the new version of IESMP. Now, together with DiPoG, we have at our disposal two independent software packages for the efficient simulation of optical gratings.

The new version of IESMP can deal with general polygonal profiles and is robust with respect to the thickness of the coated layer. To combine the short computing times of the old trigonometric Nyström method with the higher accuracy of the cubic spline algorithm, we have designed a hybrid discretization. Finally, we succeeded in developing a preconditioner of circulant pattern such that the preconditioned GMRES converges even in the difficult case of coated gratings of finite conductivity. Thanks to the iterations, the solution of the linear systems is faster than their assembling.

Fig. 1: Light intensity around a bubble between fluid and resist

In addition, we have continued to improve our FEM package DiPoG (cf. [17, 18]). In accordance with the requirements of our cooperation partners in Oberkochen, we have extended the class of echelle gratings. For application in lithography, a new code to simply generate gratings determined by an arbitrary set of profile curves has been added to the package. Moreover, we have included into our FEM package a code for the computation and the display of the light intensity in periodic diffractive structures if the latter is illuminated by coherent plane waves from multiple directions.

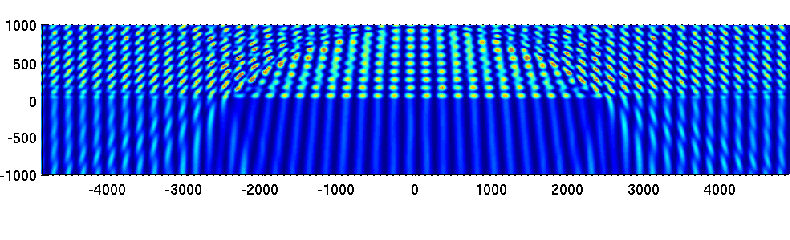
Using DiPoG, we have performed simulations of lithographic examples. Figure 1 shows the 2D simulation of the intensity distribution around a bubble (shape: segment of a circle) located between an immersion fluid and a resist area. In accordance with observations and with the FDTD simulation of A. Erdmann (Erlangen), there is a dark shadow region behind the bubble which is bounded by brighter rays. Figure 2 (left) shows a silicon bridge with square shaped cross section and with a thin layer of silicon oxide (1nm) around the bridge in the case of TM polarization, and Figure 2 (right) shows the difference of the intensity compared to the bridge without oxide layer. The lithographic applications of DiPoG are to be continued next year.

Fig. 2: Silicon bridge with oxide layer and intensity disturbance due to the oxide

For the optimization of grating profiles we have tested the global method of simulated annealing. Unfortunately, there is no fixed set of parameters working efficiently for general objective functions and profiles. Therefore and since our cooperation partners are mainly interested in small modifications of given scenarios, we now concentrate on local optimization methods. For the case of conical diffraction, we have implemented the computation of the gradient with respect to the parameters of general polygonal profile curves. The code is based upon the finite element representation developed in [3]. Currently, we are incorporating these gradient representations into conjugate gradient as well as into interior-point optimization algorithms.

2. Uniqueness results for inverse diffraction problems (J. Elschner).

In inverse scattering one is trying to reconstruct an object (an obstacle D) from observations of the scattered field generated by plane incident waves of frequency k. The field itself (acoustic or electromagnetic), in the simplest situation of scattering by a two-dimensional obstacle D, is a solution to the Helmholtz equation $\Delta$u + k²u = 0 in $\mathbb {R}$² $\setminus$ $\bar{{D}}$ satisfying the homogeneous Dirichlet boundary condition u = 0 on $\partial$D (soft obstacle) or the Neumann condition $\partial_{{\nu}}^{}$u = 0 on $\partial$D (hard obstacle). This solution is assumed to be the sum of a plane incident wave uⁱ = exp(ikx ^. d ) and a scattered wave u^s which is required to satisfy the usual Sommerfeld radiation condition at infinity. Moreover, u^s admits the representation

u^s(x) = r^-1/2u_$\infty$(x/r)exp(ikr) + O(r^-3/2), r = | x| $$\rightarrow$$ $$\infty$$,

where u_$\infty$ is called the far-field pattern.

The inverse scattering problem is to determine the obstacle D from the far-field pattern u_$\infty$ for a given frequency k and possibly several incident directions d. This problem is fundamental for exploring bodies by acoustic or electromagnetic waves, and its uniqueness (in the general 2D and 3D cases) presents important and challenging open questions since many years (see, e.g., [15]). An essential progress on uniqueness results has recently been made for polygonal and polyhedral obstacles ([2], [1]).

In [5], we considered the two-dimensional inverse scattering problem of determining a sound-hard obstacle by the far-field pattern. We established the uniqueness within the class of polygonal domains by two incoming plane waves without further geometric constraints on the scatterers. This improves the uniqueness result by Cheng and Yamamoto [2]. Refining the approach of [5], it is possible to prove uniqueness in this problem for one incident wave only, which corresponds to the result of [1] for the inverse Dirichlet problem in 2D.

Combining the methods developed in [7] and [5], we were also able to prove more general uniqueness results for inverse periodic diffraction problems. The problem of recovering a periodic structure from knowledge of the scattered field occurs in many applications in diffractive optics. We continued to study the scattering of monochromatic plane waves by a perfectly reflecting diffraction grating in an isotropic lossless medium, which is modeled by the Dirichlet problem (transverse electric polarization) or the Neumann problem (transverse magnetic polarization) for the periodic Helmholtz equation. First uniqueness theorems for 2D inverse periodic transmission problems appeared in [4]; see also Annual Research Report 2003, p. 102, for a preliminary version.

Let the profile of the diffraction grating be given by a 2$\pi$-periodic curve $\Lambda$, and suppose that a plane wave given by

uⁱ : = exp(i$$\alpha$$x₁ - i$$\beta$$x₂),($$\alpha$$,$$\beta$$) = k(sin$$\theta$$, cos$$\theta$$)

is incident on $\Lambda$ from the top, where the wave number k is a positive constant and $\theta$ $\in$ (- $\pi$/2,$\pi$/2) is the incident angle. The inverse problem or the profile reconstruction problem can be formulated as follows:

Determine the grating profile $\Lambda$ from the wave number k, possibly several incident directions $\theta$ and the scattered field on a straight line {x $\in$ $\mathbb {R}$² : x₂ = b} above the structure.

Extending the results of [7] to general piecewise linear grating profiles (which are not necessarily given by the graph of a function), we proved that a polygonal interface $\Lambda$ is always uniquely determined by two different incident directions in the Dirichlet case and by four incident waves in the Neumann case, [6]. Here we exclude the standard non-uniqueness examples of two parallels to the x₁ axis, which are not relevant for applications. Contrary to bounded obstacle scattering, it can be shown by appropriate counter examples that a smaller number of measurements is not sufficient in general. However, if one avoids the Rayleigh frequencies, then one incident direction is enough to determine the profile in the inverse Dirichlet problem.

3. Shape optimization for elliptic problems by integral equation methods (K. Eppler).

The main aim of the present work is to develop and test efficient optimization algorithms for the minimization of integral functionals, depending on the solution of an elliptic boundary value problem with a special emphasis on second-order methods. Contrary to classical control problems, the domains themselves, resp. their boundary serve as the variable or unknown in shape optimization problems. Based on a related shape calculus, complete boundary integral representations for the shape gradient and the shape Hessian provide update rules directly for the boundary. In some specific cases, integral equation methods using wavelet compression techniques for the numerical computation of the state turn out to be a powerful tool. We refer to [8], [9] for basic concepts of the proposed method. In particular, the following applications have been investigated.

• Exterior electromagnetic shaping of liquid metals. For a given external magnetic field, generated by conductors, the aim is to compute the free surface of liquid metal by means of shape optimization techniques.

  The 2D problem: A cylindrical vertical column of molten metal with a prescribed area for the cross section is falling down in a magnetic field, generated by conductors (Dirac masses or circular conductors with finite radii $\varepsilon$). The algorithm computes the unknown surface of the cross section (see [10]). Within an overall computational time of about 90 sec., the underlying PDE is solved on several dozens ( $\approx$ 50) of different exterior domains in the test cases.

  
  

  Fig. 3: Computed cross sections for Example 1 (left) and Example 2 (right)

  

  The 3D analog: The algorithm computes the shape of a bubble $\Omega$ $\subset$ R³ ( |$\Omega$|= V₀) of liquid metal, levitating in a magnetic field generated by polygonal wires (see [11]).

  
  

  Fig. 4: Resulting bubbles of liquid metal without (left)
  and with (right) gravitational force

  

• A shape identification problem from electrical impedance tomography. We implemented and tested the method for identifying a perfectly conducting obstacle within a background material of constant conductivity by measuring simultaneously voltage and current on the outer boundary. We proved the compactness of the shape Hessian at the optimal shape, which is strongly related to the known exponential illposedness of the underlying identification problem, [12]. In particular, a regularization technique for the shape Hessian provides more stability for the second-order method. We refer to [13] for the extension to 3D and related numerical results.

  
  
  

  Fig. 5: Initial guess (red) and final approximation (blue) of the inclusion for 33 Fourier coefficients in case of the regularized Newton method (left) and the quasi-
  Newton method (right). The black line indicates the outer boundary.

  

• Finally, we investigated free boundary problems, arising, for example, in chemical processing, [14]. In particular, we proved strong coercivity estimates w.r.t. H^1/2($\Gamma^{\star}_{}$) for the shape Hessian of stationary domains, implying the validity of sufficient second-order optimality conditions. Moreover, such estimates ensure numerical stability for related optimization algorithms and are important ingredients towards a convergence proof, if related finite-dimensional auxiliary optimization problems are appropriately chosen.

  
  

  Fig. 6: Computed free boundaries for Example 1 (left) and Example 2 (right)

  

References:

1. G. ALESSANDRINI, L. RONDI, Determining a sound-soft polyhedral scatterer by a single far-field measurement, to appear in: Proc. Amer. Math. Soc.

2. J. CHENG, M. YAMAMOTO, Uniqueness in an inverse scattering problem within non-trapping polygonal obstacles with at most two incoming waves, Inverse Problems, 19 (2003), pp. 1361-1384.

3. J. ELSCHNER, G. SCHMIDT, Conical diffraction by periodic structures: Variation of interfaces and gradient formulas, Math. Nachr., 252 (2003), pp. 24-42.

4. J. ELSCHNER, M. YAMAMOTO, Uniqueness results for an inverse periodic transmission problem, Inverse Problems, 20 (2004), pp. 1841-1852.

5.          , Uniqueness in determining polygonal sound-hard obstacles, to appear in: Appl. Anal.

6.          , Uniqueness in determining polygonal periodic structures, in preparation.

7. J. ELSCHNER, M. YAMAMOTO, G. SCHMIDT, An inverse problem in periodic diffractive optics: Global uniqueness with a single wave number, Inverse Problems, 19 (2003), pp. 779-787.

8. K. EPPLER, H. HARBRECHT, Numerical solution of elliptic shape optimization problems using wavelet-based BEM, Optim. Methods Softw., 18 (2003), pp. 105-123.

9.          , 2nd order shape optimization using wavelet BEM, to appear in: Optim. Methods Softw.

10.          , Exterior electromagnetic shaping using wavelet BEM, to appear in: Math. Methods Appl. Sci.

11.          , Fast wavelet BEM for 3D electromagnetic shaping, to appear in: Appl. Numer. Math.

12.          , A regularized Newton method in electrical impedance tomography using shape Hessian information, WIAS Preprint no. 943, 2004, to appear in: Control Cybernet.

13.          , Shape optimization for 3D electrical impedance tomography, WIAS Preprint no. 963, 2004, submitted.

14.          , Efficient treatment of stationary free boundary problems, WIAS Preprint no. 965, 2004, submitted.

15. V. ISAKOV, Inverse Problems for Partial Differential Equations, vol. 127 of Appl. Math. Sci., Springer, New York, 1998.

16. B. KLEEMANN, Elektromagnetische Analyse von Oberflächengittern von IR bis XUV mittels einer parametrisierten Randelementmethode: Theorie, Vergleich und Anwendungen, Forschungsberichte aus den Ingenieurwissenschaften, Mensch & Buch Verlag, Berlin, 2003.

17. A. RATHSFELD, DIPOG-2.0, User guide, Direct problems for optical gratings over triangular grids, WIAS Technical Report no. 7, 2004.
    URL: http://www.wias-berlin.de/software/DIPOG

18. G. SCHMIDT, Handbuch DIPOG-1.4, WIAS Technical Report no. 8, 2004.
    URL: http://www.wias-berlin.de/software/DIPOG

[Next]:

Optimal control of production processes

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index]