[Next]:  Algorithms for the solution of the  
 [Up]:  Projects  
 [Previous]:  Projects  
 [Contents]   [Index] 


Finite volume methods for nonlinear parabolic problems

Collaborator: J. Fuhrmann, K. Gärtner

Cooperation with: R. Eymard (Université de Marne-la-Vallée, Champs-sur-Marne, France)

Description:

We propose a new method to compute the numerical flux of a finite volume scheme, used for the approximation of the solution of the nonlinear partial differential equation

ut + $\displaystyle \nabla$($\displaystyle \vec{q} $f (u) - $\displaystyle \nabla$$\displaystyle \phi$(u)) = 0

in a 1D, 2D or 3D domain $ \Omega$.


Here, $ \vec{q} $ $ \in$ C1($ \bar{\Omega}$,$ \mathbb {R}$d) is such that div$ \vec{q} $ = 0. Furthermore, we assume $ \phi$ $ \in$ C1($ \mathbb {R}$d,$ \mathbb {R}$d) to be Lipschitz continuous and strictly monotonically increasing, and f $ \in$ C0($ \mathbb {R}$d,$ \mathbb {R}$d).

The method is based on the solution of the nonlinear elliptic two-point boundary value problem

$\displaystyle \begin{cases} \left[-\phi(v)' + q f(v)\right]' &= 0 \hbox{ on } (0,h),\\ v(0) &= a,\\ v(h) &= b, \end{cases}$ (1)
where q is the normal projection of $ \vec{q} $ onto the line connecting the centers of the control volumes.

We define a function g(a, b, q, h) by setting its value to the constant value - [$ \phi$(v(x))]' + qf (v(x)) for all x $ \in$ (0, h) for given a, b, q, h.

This function then is used to describe the numerical flux between two adjacent control volumes in a finite volume method, where a, b are the values of this solution in the adjacent control volumes.

We prove the existence of a solution to this two-point boundary value problem. We show that the expression for the numerical flux can be yielded without referring to this solution. Furthermore, we prove that the so designed finite volume scheme has the expected stability properties and that its solution converges to the weak solution of the continuous problem.

We have proven that the value of g(a, b, q, h) is given by the following relation:

\fbox{\begin{tabular}{l} if $a\le b$ then, setting $\displaystyle G_{a,b}^\flat... ...}\\ else if $a>b$ then \\ \fbox{$g(a,b,q,h) = -g(b,a,-q,h)$.} \end{tabular} }

This approach generalizes known discretization schemes like the Scharfetter-Gummel scheme to the nonlinear case.


Except in special cases, the calculation of the numerical fluxes involves the solution of nonlinear equations. To illustrate the method, we take $ \Omega$ = (0, 1), $ \phi$  : s $ \mapsto$ s2, f  : s $ \mapsto$ s, q $ \in$ [0, + $ \infty$), the initial value u0 = 0. For a given v $ \in$ (q, + $ \infty$), we use the boundary conditions at x = 0 $ \bar{u}$(0, t) = (v - q)vt/2 and set $ \bar{u}$(1, t) = 0 for t < 1/v and $ \bar{u}$(1, t) = (v - q)(vt - 1)/2, otherwise.

The unique weak solution of this problem is then given by

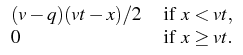
u(x, t) = $\displaystyle \left\{\vphantom{ \begin{array}{ll} (v-q) (v t-x)/2  &{\rm if} x<v t,\\ 0  &{\rm if} x \ge v t. \end{array}}\right.$$\displaystyle \begin{array}{ll} (v-q) (v t-x)/2  &{\rm if} x<v t,\\ 0  &{\rm if} x \ge v t. \end{array}$

The numerical scheme has to approximate the moving kink by a nonnegative discrete solution. The observed experimental order of convergence is shown in the following figures.


Fig. 1: Proposed scheme (left): Experimental order of convergence (EOC)=h3/2, Godunov scheme (right): EOC=h1
\makeatletter \@ZweiProjektbilderNocap[h]{0.47\textwidth}{fb04_fg3_fvol_1}{fb04_fg3_fvol_2} \makeatother

References:

  1. R. EYMARD, J. FUHRMANN, K. GÄRTNER, A finite volume scheme for nonlinear parabolic equations derived from one-dimensional local Dirichlet problems, WIAS Preprint no. 966, 2004 , submitted.


 [Next]:  Algorithms for the solution of the  
 [Up]:  Projects  
 [Previous]:  Projects  
 [Contents]   [Index] 

LaTeX typesetting by H. Pletat
2005-07-29