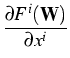Kinetic schemes for selected initial and

[Next]:

Projects interconnecting research groups

[Up]:

Projects

[Previous]:

Stability of dewetting polymer films

[Contents]

[Index]

Kinetic schemes for selected initial and boundary value problems

Collaborator: W. Dreyer, M. Herrmann, S. Qamar

Cooperation with: G. Warnecke, M. Kunik (Otto-von-Guericke-Universität Magdeburg)

Supported by: DFG: Priority Program ``Analysis und Numerik von Erhaltungsgleichungen'' (ANumE -- Analysis and numerics for conservation laws)

Description:

Within the DFG Priority Program ``Analysis and numerics of conservation laws'' we have developed and exploited a kinetic approach to solve initial and boundary value problems for some selected class of hyperbolic conservation laws. In this class there are hyperbolic conservation laws that have an underlying kinetic equation. In particular we have studied (i) the nonrelativistic Euler equations for gases, (ii) the hyperbolic system for heat conduction at low temperatures, (iii) the relativistic Euler equations with a special focus on the ultra-relativistic case. The kinetic approach relies on the Maximum Entropy Principle (MEP) and its strategy is as follows: The variables of the hyperbolic system are represented by so-called moment integrals of a corresponding phase density, which solves the underlying kinetic equation. The temporal evolution of the variables is decomposed into periods of free flight and update times. During the periods of free flight, the particles of the kinetic regime evolve according to a collision-free kinetic equation. At the update times we restart a new free flight period by maximizing the entropy of the particles.

Within the final period of the DFG Priority Program we have mainly compared the MEP method with the conventional kinetic flux-splitting schemes. We considered first-order accurate schemes as well as second-order schemes. Kinetic flux-splitting schemes also rely on the moment representation of the variables of the hyperbolic system. Here the moment integrals are decomposed into two parts with particles moving in positive and negative direction, respectively. The whole space which the particles have at their disposal is decomposed into small cells and the objective is to calculate all fluxes across the cell boundaries. In 1D the scheme is as follows:

The conservation laws have the form

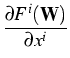$\displaystyle {\frac{{\partial\mathbf{W}}}{{\partial t}}}$ + $\displaystyle \sum\limits_{{i=1}}^{{d}}$ $\displaystyle {\frac{{\partial F^{i}(\mathbf{W})}}{{\partial x^{i}}}}$ = 0 ,

where W is the vector of conserved variables and Fⁱ are their corresponding fluxes, along each direction (d is the number of spatial dimensions).

In the one-dimensional case we decompose the x-axis into cells I_i = $\left[\vphantom{ x_{i-\frac {1}{2}},x_{i+\frac{1}{2}}}\right.$ x_i-, x_i+ $\left.\vphantom{ x_{i-\frac {1}{2}},x_{i+\frac{1}{2}}}\right]$ and study the following semi-discrete kinetic upwind scheme

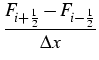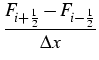$\displaystyle {\frac{{dW_{i}}}{{dt}}}$ = - $\displaystyle {\frac{{F_{i+\frac{1}{2}}-F_{i-\frac{1}{2}}}}{{\Delta x}}}$ .

Thus a first-order scheme which is fully discrete in space and time is given by

W_iⁿ⁺¹ = W_iⁿ - $\displaystyle \lambda$ $\displaystyle {\frac{{F_{i+\frac{1}{2}}-F_{i-\frac{1}{2}}}}{{\Delta x}}}$ ,

where $\lambda$ = ${\frac{{\Delta t}}{{\Delta x}}}$ , F_i+ is the fluxes at the cell boundary x_i+. Here W_iⁿ are the piecewise constant cell average values of the conserved variables at time tⁿ, and $\Delta$ x represents the cell width.

This scheme is only first-order accurate in space. To get high-order accuracy, the initial reconstruction strategy must be applied to interpolate the cell-averaged variables W_iⁿ.

For example,

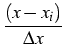
W(tⁿ, x) = W_iⁿ + W_i^{n, x} $\displaystyle {\frac{{(x-x_{i})}}{{\Delta x}}}$

can be constructed to approximate the cell-averaged variables W_iⁿ at the beginning of each time step tⁿ, where W_i^{n, x} is an approximate slope. The extreme points x = 0 and x = $\Delta$ x in local coordinates correspond to the intercell boundaries in general coordinates x_i- and x_i+, respectively. The values W_i at the extreme points are

W_i^{n, L} = W_iⁿ - $\displaystyle {\frac{{1}}{{2}}}$ W_i^{n, x} , W_i^{n, R} = W_iⁿ + $\displaystyle {\frac{{1}}{{2}}}$ W_i^{n, x} .

(1)

To avoid oscillations in the reconstructed data, the slope W_i^{n, x} is obtained from the min-mod limiter as follows

W_i^x = MM $\displaystyle \left(\vphantom{ \theta\Delta W_{i+\frac{1}{2}},\frac{\theta}{2}(... ...i-\frac{1}{2}}+\Delta W_{i+\frac{1}{2}}),\theta\Delta W_{i-\frac{1}{2}}}\right.$ $\displaystyle \theta$ $\displaystyle \Delta$ W_i+, $\displaystyle {\frac{{\theta}}{{2}}}$ ( $\displaystyle \Delta$ W_i- + $\displaystyle \Delta$ W_i+), $\displaystyle \theta$ $\displaystyle \Delta$ W_i- $\displaystyle \left.\vphantom{ \theta\Delta W_{i+\frac{1}{2}},\frac{\theta}{2}(... ...i-\frac{1}{2}}+\Delta W_{i+\frac{1}{2}}),\theta\Delta W_{i-\frac{1}{2}}}\right)$ .

Here, $\Delta$ denotes the central differencing, $\Delta$ W_i+ = W_i+1 - W_i, and MM denotes the min-mod nonlinear limiter

MM{x₁, x₂,...} = $\displaystyle \left\{\vphantom{ \begin{array}[c]{ll}% \mbox{min}_{i}\{x_{i}\}\q... ...\quad\forall i\,, & \\ 0\qquad\qquad\mbox{otherwise}\,. & \end{array}}\right.$ $\displaystyle \begin{array}[c]{ll}% \mbox{min}_{i}\{x_{i}\}\quad\mbox{if\,\,}x_... ...}x_{i}<0\quad\forall i\,, & \\ 0\qquad\qquad\mbox{otherwise}\,. & \end{array}$ ,

(2)

where 1 $\leq$ $\theta$ $\leq$ 2 is a parameter. Based on the above reconstruction, a high spatial resolution kinetic solver becomes

$\displaystyle {\frac{{dW_{i}}}{{dt}}}$ = - $\displaystyle {\frac{{F_{i+\frac{1}{2}}(W_{i+1}^{L},W_{i}^{R}% )-F_{i-\frac{1}{2}}(W_{i}^{L},W_{i-1}^{R})}}{{\Delta x}}}$ ,

(3)

where W^l, W^R are given by (1).
To improve the temporal accuracy, we use a second-order TVD Runge-Kutta scheme to solve (3). Denoting the right-hand side of (3) as L(W), a second-order TVD Runge-Kutta scheme updates W through the following two stages:
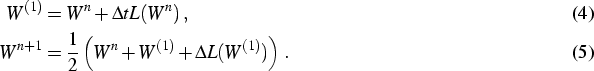
$\begin{align} W^{(1)} & =W^{n}+\Delta t L(W^{n}) ,\\ W^{n+1} & =\frac12 \left( W^{n}+W^{(1)}+\Delta L(W^{(1)})\right) . \end{align}$

References:

W. DREYER, M. HERRMANN, S. QAMAR, Kinetic schemes for selected initial and boundary value problems, WIAS Preprint no. 880, 2003 , to appear in: ANumE Proceedings.
W. DREYER, S. QAMAR, Second order accurate explicit finite volume schemes for the solution of Boltzmann-Peierls equation, to appear in: Z. Angew. Math. Mech.
, Kinetic flux-vector splitting schemes for the hyperbolic heat conduction, to appear in: J. Comput. Phys.
M. KUNIK, S. QAMAR, G. WARNECKE, Kinetic schemes for the ultra-relativistic Euler equations, J. Comput. Phys., 1066187 (2003), pp. 572-596.
, Kinetic schemes for the relativistic gas dynamics, Preprint no. 02-21, Fakultät für Mathematik, Universität Magdeburg, 2002, to appear in: Numer. Math.
, A BGK-type kinetic flux-vector splitting scheme for the ultra-relativistic Euler equations, Preprint no. 03-04, Fakultät für Mathematik, Universität Magdeburg, 2003, to appear in: J. Sci. Comput.